 por leo_30_rj » Sáb Ago 14, 2010 17:17
por leo_30_rj » Sáb Ago 14, 2010 17:17
PESSOAL, BOA TARDE
ESSE PROBLEMA PARECE FÁCIL, MAS....
QUESTÃO) A METADE DE UM CAPITAL C FOI APLICADO A JUROS COMPOSTOS COM TAXA DE 20% A.M. SIMULTANEAMENTE, A OUTRA METADE FOI APLICADA A JUROS SIMPLES COM TAXA MENSAL DE i%. AO FINAL DE 2 MESES, OS MONTANTES A JUROS SIMPLES E JUROS COMPOSTOS FORAM SOMADOS E SEU VALOR CORRESPONDIA AO CAPITAL TOTAL C, ACRESCIDO DE 50%. QTOS. SÃO OS DIVISORES INTEIROS POSITIVOS DE i?
BOM, EU USEI AS FORMULAS DE JUROS SIMPLES E COMPOSTO E MONTEI AS EQUAÇÕES....TUDO BLZ!
A TAXA I% QUE ENCONTREI FOI 14% - MINHA RESPOSTA: 4, POIS OS DIVISORES DE 14 SÃO: 1, 2, 7 E 14.
SÓ QUE A RESPOSTA FINAL CORRETA É 6!!!!
POR FAVOR, SE PUDEREM AJUDAR EU AGRADEÇO.
OBRIGADO
-
leo_30_rj
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Seg Jul 26, 2010 03:13
- Formação Escolar: GRADUAÇÃO
- Área/Curso: outros
- Andamento: cursando
 por alexandre32100 » Sáb Ago 14, 2010 18:05
por alexandre32100 » Sáb Ago 14, 2010 18:05
-
alexandre32100
-
 por Douglasm » Seg Ago 16, 2010 13:59
por Douglasm » Seg Ago 16, 2010 13:59
Alexandre, acho que você esqueceu de considerar que metade do capital é acrescido dos respectivos juros e de considerar o capital inicial no caso dos juros simples. Note só:
![\frac{C}{2}.(1 + 0,20)^2 + [\frac{C}{2} + 2.\frac{C}{2}.i] = 1,50 C \;\therefore \frac{C}{2}.(1 + 0,20)^2 + [\frac{C}{2} + 2.\frac{C}{2}.i] = 1,50 C \;\therefore](/latexrender/pictures/410ab333f9eb36e0ef5890b325f30018.png)


Sendo assim, os divisores são 1, 2, 4, 7, 14 e 28.
Até a próxima.
-

Douglasm
- Colaborador Voluntário

-
- Mensagens: 270
- Registrado em: Seg Fev 15, 2010 10:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Matemática Financeira
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Descobrindo os casais
por Cleyson007 » Dom Fev 07, 2010 14:18
- 1 Respostas
- 1480 Exibições
- Última mensagem por Elcioschin

Seg Fev 08, 2010 22:37
Desafios Médios
-
- Integral Descobrindo valores.
por Maykids » Qua Jun 29, 2011 12:33
- 1 Respostas
- 1638 Exibições
- Última mensagem por LuizAquino

Qua Jun 29, 2011 16:22
Cálculo: Limites, Derivadas e Integrais
-
- Limites descobrindo Valores
por Maykids » Sáb Jul 09, 2011 01:19
- 1 Respostas
- 1060 Exibições
- Última mensagem por LuizAquino

Ter Jul 12, 2011 11:36
Cálculo: Limites, Derivadas e Integrais
-
- equação de segundo grau( descobrindo as raizes)
por arturmedeiros2010 » Qui Fev 13, 2014 15:34
- 1 Respostas
- 1359 Exibições
- Última mensagem por Russman

Sex Fev 14, 2014 00:15
Equações
-
- Descobrindo a Expressão Algébrica olhando apenas o gráfico
por Ricardogferreira » Seg Jul 23, 2012 21:19
- 12 Respostas
- 12413 Exibições
- Última mensagem por Ricardogferreira

Ter Jul 31, 2012 20:25
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


![[C\cdot (1+i)^{t}-C]+Cit=\dfrac{C}{2} [C\cdot (1+i)^{t}-C]+Cit=\dfrac{C}{2}](/latexrender/pictures/4129df99579d79e74b5e3dbcfd86c080.png)
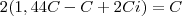
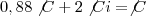
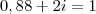
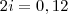
 ou
ou 
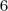 são
são  .
. .
.![\frac{C}{2}.(1 + 0,20)^2 + [\frac{C}{2} + 2.\frac{C}{2}.i] = 1,50 C \;\therefore \frac{C}{2}.(1 + 0,20)^2 + [\frac{C}{2} + 2.\frac{C}{2}.i] = 1,50 C \;\therefore](/latexrender/pictures/410ab333f9eb36e0ef5890b325f30018.png)


