Olá, até que sei as fórmulas, mas estou com dúvida em relação ao tempo e à montagem da questão...
FCC) Uma duplicata no valor de R$ 6900,00 foi resgatada 3 meses antes de seu vencimento. Considerando que a taxa anual de desconto comercial simples foi de 48%, então, se o valor atual dessa duplicata era X reais, é correto afirmar que
a) X <= (é menor ou igual a) 5700
b) 5700 < X <= 5800
c) 5800 < X <= 5900
d) 5900 < X <= 6000
e)X > 6000
O que quiseram dizer com "3 meses antes de seu vencimento" - o tempo é 3 meses ou 9 meses ?
"D= N . i . t"
N= 6900
t= ???
i= 0,48
"Dr= Ar . ir. t " ou poderia usar, "N= D+ Ar"


 o capital atual oriundo de um valor
o capital atual oriundo de um valor  .
.  .
.  .
. 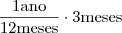 .
. 


![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)