 por DanielRJ » Qui Out 21, 2010 15:32
por DanielRJ » Qui Out 21, 2010 15:32
(TTN/18985) Se 6/8 de uma quantia produzem 3/8 desta mesma quantia de juros em 4 anos , qual a taxa aplicada?
resp)12,5% a.a
Eu entendi assim:
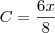
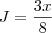


mesmo assim não vai...
-

DanielRJ
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Sex Ago 20, 2010 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por thayna » Qui Out 21, 2010 17:30
por thayna » Qui Out 21, 2010 17:30
Olá, boa tarde.
Olha, você não precisa usar o (x)
então fica assim:
c= 6/8
t=4
j=3/8
i=?
aii vc põe esses valores na fómula j=cit.
da um resultado de 0,125 mas como é taxa, tranforma-se em porcentagem, ficando 12,5% a.a
-
thayna
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Qui Out 21, 2010 17:20
- Formação Escolar: ENSINO FUNDAMENTAL II
- Andamento: cursando
 por DanielRJ » Qui Out 21, 2010 17:57
por DanielRJ » Qui Out 21, 2010 17:57
thayna escreveu:Olá, boa tarde.
Olha, você não precisa usar o (x)
então fica assim:
c= 6/8
t=4
j=3/8
i=?
aii vc põe esses valores na fómula j=cit.
da um resultado de 0,125 mas como é taxa, tranforma-se em porcentagem, ficando 12,5% a.a
obgdo ..mas queria saber porque não se pode usar o x.
-

DanielRJ
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Sex Ago 20, 2010 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por MarceloFantini » Qui Out 21, 2010 18:23
por MarceloFantini » Qui Out 21, 2010 18:23
Pode usar sim.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por thayna » Qui Out 21, 2010 18:27
por thayna » Qui Out 21, 2010 18:27
pode usar, eu só falei que não precisava
-
thayna
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Qui Out 21, 2010 17:20
- Formação Escolar: ENSINO FUNDAMENTAL II
- Andamento: cursando
 por DanielRJ » Sex Out 22, 2010 15:21
por DanielRJ » Sex Out 22, 2010 15:21
obrigado pessoal não conseguia por um detalhe..esqueci de simplificar a primeira fração
-

DanielRJ
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Sex Ago 20, 2010 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Matemática Financeira
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Juros Simples // Juros Compostos
por Roberta » Qui Jul 16, 2009 18:22
- 3 Respostas
- 8209 Exibições
- Última mensagem por Roberta

Qui Jul 16, 2009 19:46
Matemática Financeira
-
- Juros Simples
por Gir » Ter Set 01, 2009 11:03
- 1 Respostas
- 8303 Exibições
- Última mensagem por Lucio Carvalho

Ter Set 01, 2009 17:24
Matemática Financeira
-
- juros simples
por sandi » Seg Out 05, 2009 23:58
- 1 Respostas
- 3748 Exibições
- Última mensagem por DanielFerreira

Seg Mar 29, 2010 11:49
Matemática Financeira
-
- Juros Simples
por Livia Primo » Seg Mar 15, 2010 19:13
- 1 Respostas
- 4743 Exibições
- Última mensagem por DanielFerreira

Seg Mar 15, 2010 19:20
Pedidos
-
- JUROS SIMPLES
por Liliani » Seg Abr 05, 2010 17:47
- 5 Respostas
- 6470 Exibições
- Última mensagem por aldhemah

Qua Abr 07, 2010 00:19
Desafios Médios
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
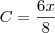
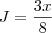



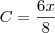
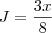










 , avisa que eu resolvo.
, avisa que eu resolvo.

