Olá,
estou tendo muita dificuldade em resolver um problema de Juros compostos, devido não saber encontrar a taxa mensal,mesmo tendo a fórmula. Tentei resolver usando o binômio de newton, mas parece que não é desta forma. Vejam o problema:
*Um título de crédito no valor de R$ 2000,00 foi resgatado 4 meses antes do seu vencimento, obtendo um desconto de R$ 100,00, adotando o critério de desconto comercial composto, então o valor da taxa mensal é:
[i]a) 0,5% a.m.
b) 1,07% a.m.
c) 1,27% a.m.
d) 1,62% a.m.
e) 2% a.m.
Fórmula que acredito que deva ser usada:
d= N[1-(1-i)^n]
resposta correta: c
Obrigado!
)
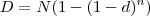, onde:![\\100=2000(1-(1-d)^4)\\
\frac{100}{2000}=1-(1-d)^4\\
(1-d)^4=1-\frac{100}{2000}\\
(1-d)^4=\frac{1900}{2000}\\
1-d=\sqrt[4]{\frac{1900}{2000}}\\
1-d\approx 0,987259\\
d\approx 1-0,987259\\
d\approx 0,012741=1,2741\%\text{a.m.}](/latexrender/pictures/801d09382202bc85a72fa4685fd0c1f4.png "\\100=2000(1-(1-d)^4)\\
\frac{100}{2000}=1-(1-d)^4\\
(1-d)^4=1-\frac{100}{2000}\\
(1-d)^4=\frac{1900}{2000}\\
1-d=\sqrt[4]{\frac{1900}{2000}}\\
1-d\approx 0,987259\\
d\approx 1-0,987259\\
d\approx 0,012741=1,2741\%\text{a.m.}")
".
.
, 
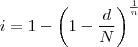
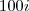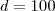e 
.
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
e elevar ao quadrado os dois lados)