Boa tarde, Estou fazendo Faculdade de logística e tenho essa materia Matematica Financeira, tenho que fazer a prova e estou estudando se alguem poder me orientar Agradeço desde ja..
Segue a Pergunta;
Um trilho de 20m de comprimento sofre um alongamento de 3mm, para um acréscimo de temperatura de 16°C. Determine o alongamento sofrido por um trilho de 14m de comprimento, para um acréscimo de temperatura de 20°C.
att;
Itamar


 ) é diretamente proporcional ao comprimento inicial do trilho(
) é diretamente proporcional ao comprimento inicial do trilho(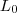 ) e a variação de temperatura (
) e a variação de temperatura (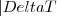 ). Assim, podemos escrever
). Assim, podemos escrever 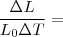 constante.
constante. e
e  para situações diferentes temos a igualdade
para situações diferentes temos a igualdade .
.
 na unidade mm, pois esta é a que usamos para
na unidade mm, pois esta é a que usamos para  . É importante lembrar que essa "mistura" de unidades (mm com m) só se pode ser feita pois estamos tratando de proporção de modo que as razões entre as unidades se simplificam não havendo necessidade de transforma-las.
. É importante lembrar que essa "mistura" de unidades (mm com m) só se pode ser feita pois estamos tratando de proporção de modo que as razões entre as unidades se simplificam não havendo necessidade de transforma-las.

 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.