




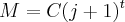

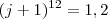
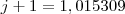




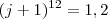 , precisamos tirar a raíz 12ª pois o (j+1) está elevado na 12 e queremos deixá-lo no expoente 1, só j+1 para poder trabalhar melhor com esses números. Para eliminar esse expoente 12, temos que tirar a raíz 12ª. Só que se tirarmos a raíz 12ª do j+1, precisamos tirar também do 1,2. Não dá pra operar isso só num lado sem mexer no outro, entende?
, precisamos tirar a raíz 12ª pois o (j+1) está elevado na 12 e queremos deixá-lo no expoente 1, só j+1 para poder trabalhar melhor com esses números. Para eliminar esse expoente 12, temos que tirar a raíz 12ª. Só que se tirarmos a raíz 12ª do j+1, precisamos tirar também do 1,2. Não dá pra operar isso só num lado sem mexer no outro, entende?![\sqrt[12]{(j+1)^{12}} = \sqrt[12]{1,2} \sqrt[12]{(j+1)^{12}} = \sqrt[12]{1,2}](/latexrender/pictures/3bc02ed0d9e30c58b0b8e932ebd38b82.png)
![\sqrt[12]{1,2} = 1,2^{\frac{1}{12}} = 1,2^{0,08333...} \sqrt[12]{1,2} = 1,2^{\frac{1}{12}} = 1,2^{0,08333...}](/latexrender/pictures/bf69301b644830f95a2b4ea383fd1532.png)




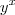 .
.

 é fácil pois é a mesma coisa que
é fácil pois é a mesma coisa que ![\sqrt[]{4} \sqrt[]{4}](/latexrender/pictures/c9134ba422cb8352ff186028fe0cbdfc.png) . O resultado vai ser 2, pois 2x2 é 4.
. O resultado vai ser 2, pois 2x2 é 4.











Gir escreveu:Qual sera o montante produzido pelo capital de R$ 20.000,00 ,aplicado a juros compostos,à taxa de 20% ao ano,durante 6 meses?
esta pedindo o tempo em meses,mas a taxa de juros esta em ano!como eu faço?

Voltar para Matemática Financeira
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.