30. As economias de um clube foram aplicadas por 2 anos e meio com taxa de 2,5% ao mês, no regime
de juros simples. Ao final da aplicação, obteve-se o valor total de R$ 7.350,00. O valor aplicado foi
(A) R$ 4.000,00.
(B) R$ 4.200,00.
(C) R$ 4.400,00.
(D) R$ 4.600,00.
j=cit
7350=c(0,025+30)
7350=0,75c
c=9800 mesmo se eu subtrair 7350 nao da 4200(alternatica certa)
a formula de montante:
m=c(1+0,025+30)
c=236,90(nada a ver)
vejam:
j=4200*0.025*30=3015 subtraindo 7350 da 4200 como eu acho esse 3015 pra achar esse 4200 meu pai?
pireei'


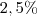 ao mês durante
ao mês durante 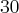 meses, então
meses, então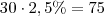
 terá rendimento
terá rendimento 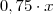 no periodo.
no periodo.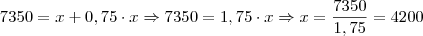
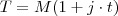 sendo T=total; M=montante, j=Juros, t=Tempo
sendo T=total; M=montante, j=Juros, t=Tempo

 .
.
 :
: