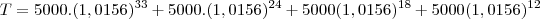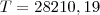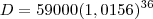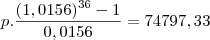por ronaldoacj » Ter Out 30, 2012 14:16
por ronaldoacj » Ter Out 30, 2012 14:16
Ana Clara, responsável pelo setor de logística de uma renomada empresa da região de Contagem, verificou a necessidade de adquirir mais um caminhão para compor a frota e melhorar o tempo de entrega dos produtos. Fez uma pesquisa de mercado e a empresa cujo valor à vista do equipamento estava mais barato oferecia-o por R$59.000. A proposta de venda para pagamento parcelado consistia em efetuar 36 pagamentos mensais, iguais e postecipados, sendo realizados 04 pagamentos de parcelas intermediárias, cada uma no valor de R$5.000,00 acontecendo em 3, 12, 18 e 24 meses, ou seja, nesses meses além de pagar o valor da prestação, Ana Clara ainda deveria arcar com a quantia “extra” de R$5.000,00. Com base nesses dados, pede-se: determinar o valor das prestações a serem pagas por Ana Clara, considerando uma taxa de juros compostos de 1,56% a.m
-
ronaldoacj
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Sex Out 26, 2012 11:53
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Sistemas de Informação
- Andamento: cursando
 por young_jedi » Ter Out 30, 2012 17:59
por young_jedi » Ter Out 30, 2012 17:59
primeiro voce tem que calcular quanto vai reder o pagamento de R$ 5000,00 levando em consideração o mes do pagamento e o juros mensal
o primerio mes de pagamento de 5000 ocorre no mes 3 portanto o total de meses de juros sobre ele sera 36-3=33
para o segundo mes temos que ele ocorre no mes 12 portanto o total de meses de juros sobre ele sera 36-12=24
assim calculamos tambem o terceiro e quarto pagamentos, portanto o total calculado com juros sera
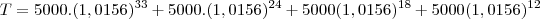
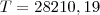
agora clacular quanto a divida de 59000 vai aumentar ao longo desses 36 meses
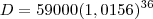

agora fazendo a subtração da divida e do total pago

esta é a divida a ser quitada com as demais prestações mensais.
então utilizaremos este valor para clacular o valor das parcelas levando em conta que sera paga uma a cada mes ao longo de 36 meses
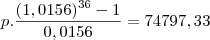

acho que é isso, comente qualquer duvida
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por ronaldoacj » Ter Out 30, 2012 18:23
por ronaldoacj » Ter Out 30, 2012 18:23
Ola,
Eu vi um exercicio que segue abaixo com a resolução:
a) elaborar um texto explicando a condição de pagamento proposta;
Essa é uma série de pagamentos, também chamada de rendas certas ou anuidades,
por ser composta por prestações periódicas e uniformes. O pagamento é composto
por uma entrada, prestações fixas e um pagamento intermediário, a saber:
- Entrada de R$7.500,00;
- 10 prestações mensais fixas de R$1.602,32;
- 01 parcela intermediária, também chamada de parcela “balão”, no valor de
R$1.000,00 acontecendo junto com o pagamento da quinta parcela.
b) determinar o valor financiado, sabendo que a taxa do financiamento é de
1,75% ao mês.
Para determinar o valor financiado, ou seja, o valor à vista do bem é necessário dividir
o problema em três etapas: descapitalização das prestações, descapitalização da
parcela intermediária e por fim a soma desses valores descapitalizados à entrada,
resultando, assim no valor presente (data zero) do bem.
Portanto, seguindo esse raciocinio eu pensei que eu deveria descapitalizar os valores de $5 mil e subtrair do montante de $59 mil capitalizado no periodo de 36 meses.
Não seria isso?
-
ronaldoacj
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Sex Out 26, 2012 11:53
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Sistemas de Informação
- Andamento: cursando
 por young_jedi » Ter Out 30, 2012 20:05
por young_jedi » Ter Out 30, 2012 20:05
é isso mesmo
a diferença é que neste não existe a entrada
se voce reparar oque eu fiz foi separar em duas partes onde em uma delas eu calculo o valor das prestações de 5000 capitalizadas e o valor dos 59000 capitalizados e subtrai um do outro, então sabemos que esse valor e o valor das mensalidades capitalizadas
realizando a descpitalização temos os valores das parcelas
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por ronaldoacj » Qua Out 31, 2012 13:57
por ronaldoacj » Qua Out 31, 2012 13:57
Young_jedi,
Como no exemplo que mostrei, houve a descapitalização, pois havia juros sobre o valor de $1 mil reais. Não seria o mesmo caso com o $5 mil? Havendo o juros o correto seria descapitalizar, não?
Desculpe a insistência! =/
Abs.
-
ronaldoacj
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Sex Out 26, 2012 11:53
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Sistemas de Informação
- Andamento: cursando
 por young_jedi » Qua Out 31, 2012 18:11
por young_jedi » Qua Out 31, 2012 18:11
No exercicio exemplo que voce mostrou, voce tinha os valores das prestações e queria determinar o valor inicial
neste caso ele quer determinar as prestações, sendo que ele fornece o valor inicial e as prestações intermediarias
portanto voce tem que calcular quanto o pagamento das intermediarias rende e quanto de juros incide sobre o valor inicial, para que assim voce determina quanto ainda resta a pagar, e assim determinar os valores das prestações mensais que devem quitar este valor.
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
Voltar para Matemática Financeira
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Série uniforme de pagamentos (postecipada)
por uarl » Ter Jun 14, 2011 23:49
- 1 Respostas
- 2865 Exibições
- Última mensagem por carlosmagnodg

Qua Jun 15, 2011 15:53
Matemática Financeira
-
- [Série financeira diferida]
por mnds109 » Sáb Mai 14, 2016 21:36
- 0 Respostas
- 1141 Exibições
- Última mensagem por mnds109

Sáb Mai 14, 2016 21:36
Matemática Financeira
-
- MATEMÁTICA FINANCEIRA - Equivalência financeira
 por ivolatanza » Ter Fev 28, 2017 15:33
por ivolatanza » Ter Fev 28, 2017 15:33
- 0 Respostas
- 10478 Exibições
- Última mensagem por ivolatanza

Ter Fev 28, 2017 15:33
Matemática Financeira
-
- Matemática Financeira
por plugpc » Sáb Jun 13, 2009 16:58
- 0 Respostas
- 9314 Exibições
- Última mensagem por plugpc

Sáb Jun 13, 2009 16:58
Vestibulares
-
- matematica financeira
por Joziani » Qui Abr 22, 2010 23:18
- 1 Respostas
- 6347 Exibições
- Última mensagem por Molina

Sex Abr 23, 2010 00:07
Matemática Financeira
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.