Numa razão,a diferença entre o antecedente e o consequente é 9 e o dobro do consequente mais o antecedente é 57.Então a razão é:
R:25/16



Valmel escreveu:Numa razão,a diferença entre o antecedente e o consequente é 9 e o dobro do consequente mais o antecedente é 57.Então a razão é:
R:25/16
 , onde:
, onde: é o antecedente;
é o antecedente;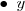 é o consequente;
é o consequente;

danjr5 escreveu:Valmel escreveu:Numa razão,a diferença entre o antecedente e o consequente é 9 e o dobro do consequente mais o antecedente é 57.Então a razão é:
R:25/16
 , onde:
, onde: é o antecedente;
é o antecedente;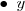 é o consequente;
é o consequente;

Valmel escreveu: 1° que função no teclado eu uso pra digitar estas chaves grandes?
Valmel escreveu:2° Acho que este,eu posso resolver pela substituição e adição;
Valmel escreveu:3°Se substituição, eu resolvo(o correto é 2y + x = 57) que resulta 19, aí como eu substituo na outra 19 - y = 9 que dá, peraí o y fica negativo e eu multiplico sempre por -1 pra ficar positivo e eu tenho 28, dái em diante como faço?
 , agora devemos isolá-la;
, agora devemos isolá-la;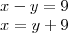
 da outra equação (
da outra equação (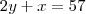 ), será substituído por
), será substituído por  ;
;
 ) em qualquer equação obtemos:
) em qualquer equação obtemos: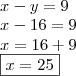
Valmel escreveu:4°se adição,é fácil somar aquelas que x fica debaixo de x mas esta com x sob - y,como eu vou eliminar?
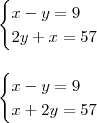
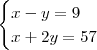



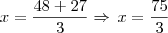
 , temos:
, temos: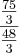
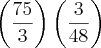
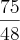
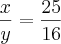
 É assim que chegamos aonde queremos!
É assim que chegamos aonde queremos!
Voltar para Matemática Financeira
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
zig escreveu:

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.