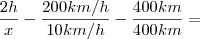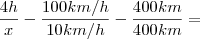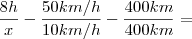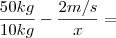por mark_adm » Sáb Mai 12, 2012 22:13
por mark_adm » Sáb Mai 12, 2012 22:13
Olá boa-noite! Tenho um trabalho de Matématica para entregar nesta terça-feira dia 15/05, mas há três questões que eu não consigo resolver: a 3, a 7 e a 8. Estão logo abaixo. Me respondam o mais rápido possível.
3) A Distância entre as cidades de São Paulo e Rio de Janeiro é de 400km. Se um carro mantiver a velocidade constante de 200 km/h, então, em duas horas, ele fará o percurso entre São Paulo e Rio de Janeiro. Se o carro mantiver a velocidade constante de 100 km/h, fará o percurso em quatro horas. Caso seja 50 km/h, o tempo gasto será de oito horas. Se o carro mantiver a velocidade de 25km/h, fará o percurso em 16 horas. Se ele mantiver uma velocidade de 10 km/h, em quanto tempo fará o percurso?
7) As Grandezas Força F e e Aceleração A são diretamente proporcionais para uma Massa M constante pela fórmula: F= M x A. Comuma aceleração de 10 m/s², obteve-se força de 50N (newtons). Qual será a força para uma aceleração de 5 m/s²?
8) No caso do exercício anterior, sabe-se que para uma Força F constante, se a massa aumentar, a velocidade será reduzida. Se uma massa de 50 kg corresponde a uma aceleração de 2 m/s², então se a massa for de 10 kg, qual será a aceleração?
-
mark_adm
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Sáb Mai 12, 2012 21:16
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por Fabiano Vieira » Sáb Mai 12, 2012 23:48
por Fabiano Vieira » Sáb Mai 12, 2012 23:48
mark_adm escreveu:A Distância entre as cidades de São Paulo e Rio de Janeiro é de 400km. Se um carro mantiver a velocidade constante de 200 km/h, então, em duas horas, ele fará o percurso entre São Paulo e Rio de Janeiro
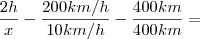
mark_adm escreveu: Se o carro mantiver a velocidade constante de 100 km/h, fará o percurso em quatro horas
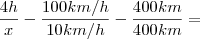
mark_adm escreveu:Caso seja 50 km/h, o tempo gasto será de oito horas
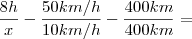
Você precisava pegar somente uma caso para comparar na regra de três. Pois note que nos exemplos acima, o resultado será o mesmo.
-
Fabiano Vieira
- Usuário Parceiro

-
- Mensagens: 69
- Registrado em: Seg Abr 16, 2012 23:11
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Sistema de Informação
- Andamento: cursando
 por Fabiano Vieira » Dom Mai 13, 2012 00:11
por Fabiano Vieira » Dom Mai 13, 2012 00:11
mark_adm escreveu:As Grandezas Força F e e Aceleração A são diretamente proporcionais para uma Massa M constante pela fórmula: F= M x A. Comuma aceleração de 10 m/s², obteve-se força de 50N (newtons). Qual será a força para uma aceleração de 5 m/s²?

-
Fabiano Vieira
- Usuário Parceiro

-
- Mensagens: 69
- Registrado em: Seg Abr 16, 2012 23:11
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Sistema de Informação
- Andamento: cursando
 por Fabiano Vieira » Dom Mai 13, 2012 00:33
por Fabiano Vieira » Dom Mai 13, 2012 00:33
mark_adm escreveu:No caso do exercício anterior, sabe-se que para uma Força F constante, se a massa aumentar, a velocidade será reduzida. Se uma massa de 50 kg corresponde a uma aceleração de 2 m/s², então se a massa for de 10 kg, qual será a aceleração?
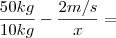
-
Fabiano Vieira
- Usuário Parceiro

-
- Mensagens: 69
- Registrado em: Seg Abr 16, 2012 23:11
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Sistema de Informação
- Andamento: cursando
 por geraldo » Seg Mai 14, 2012 12:33
por geraldo » Seg Mai 14, 2012 12:33
Fabiano Vieira escreveu:mark_adm escreveu:No caso do exercício anterior, sabe-se que para uma Força F constante, se a massa aumentar, a velocidade será reduzida. Se uma massa de 50 kg corresponde a uma aceleração de 2 m/s², então se a massa for de 10 kg, qual será a aceleração?
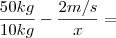
três sócios formaram uma sociedade entrando cada um com as quantias R$5.000, R$8.000 e R$8.000 respectivamente. O primeiro permaneceu na sociedade por 12 meses, o segundo por 7 meses e o terceiro por 5 meses. O prejuízo dessas operações foi de R$46.800. Qual o prejuízo menor dos três?
-
geraldo
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Seg Mai 14, 2012 12:20
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Matemática Financeira
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Grandezas Diretamente e Inversamente Proporcionais
por Jhenrique » Seg Out 15, 2012 13:13
- 4 Respostas
- 2595 Exibições
- Última mensagem por Jhenrique

Seg Nov 05, 2012 13:55
Álgebra Elementar
-
- preciso de ajuda urgente!!!!
 por matematicada » Qua Nov 24, 2010 12:17
por matematicada » Qua Nov 24, 2010 12:17
- 2 Respostas
- 2075 Exibições
- Última mensagem por matematicada

Qui Nov 25, 2010 11:39
Funções
-
- preciso de ajuda, é urgente
por nayane » Sex Nov 26, 2010 21:12
- 2 Respostas
- 2033 Exibições
- Última mensagem por nayane

Sáb Nov 27, 2010 14:40
Álgebra Elementar
-
- Preciso de Ajuda com Limites - URGENTE!!!
por Josi » Qui Set 10, 2009 17:34
- 4 Respostas
- 3615 Exibições
- Última mensagem por Josi

Qui Set 10, 2009 18:40
Cálculo: Limites, Derivadas e Integrais
-
- preciso de ajuda urgente por favor
por weverton » Qua Jun 23, 2010 17:56
- 0 Respostas
- 1495 Exibições
- Última mensagem por weverton

Qua Jun 23, 2010 17:56
Matemática Financeira
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.