Problema "João"

por **michajunco** » Ter Jul 12, 2011 17:15

Olá, estou resolvendo um exercicio mas empaquei em uma pergunta.
O exercicio é o seguinte, João comprou hoje um equipamento por 2000,00. A cada ano os equipamentos novos sofrem aumento de 8% em relacao ao ano anterior e, os usados sofrem depreciação de 19% ao ano.
Enfim, cheguei às equações que fornecem o preço, em reais, de um equipamento novo e de um usado, respectivamente:
$N(t)=2000.{1,08}^{t}\; J(t)=2000.{0,81}^{t}$
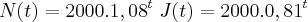
Agora o problema pede: "O numero inteiro minimo de anos que deverão decorrer a partir de hoje, para que o valor do equipamento usado por João se torne inferior a 10% do preço de um equipamento novo."

Que equacao devo formar?

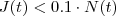por **MarceloFantini** » Ter Jul 12, 2011 17:36

Você terá que encontrar os valores de t tais que $J(t) < 0.1 \cdot N(t)$ .

Problema "João"

Problema "João"

Problema "João"

Re: Problema "João"

Quem está online