Em geral, apenas enunciados de exercícios.
Regras do fórum
- Não envie somente enunciados de problemas, informe suas tentativas e dificuldades!
Queremos que a "ajuda" represente um trabalho interativo, pois saber especificar a dúvida exige estudo.
Serão desconsiderados tópicos apenas com enunciados, sem interação. Nosso objetivo não é resolver listas de exercícios;
- Para não haver má interpretação em suas postagens, especialmente na precedência das operações, utilize LaTeX, podendo ser a partir do botão "editor de fórmulas".
Bons estudos!
 por Julie » Qua Jul 28, 2010 10:00
por Julie » Qua Jul 28, 2010 10:00
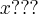
Num dia, um pintor pinta 2/5 de um muro.No dia seguinte,pinta mais 51 metros do muro.Desse modo,pintou 7/9 do muro todo.Quantos metros tem o muro?
OBS:Tenho dificuldade em interpretar o problema e assim não consigo desenvolve-lo.Sera que tem alguma regra em geral
para que eu consiga montar não só esse como outros.
*Quando montado o problema eu consigo desenvolve-lo*
-
Julie
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Ter Jul 27, 2010 00:13
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: gestão em recursos humanos
- Andamento: cursando
 por Julie » Qua Jul 28, 2010 10:06
por Julie » Qua Jul 28, 2010 10:06
Julie escreveu: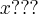
Num dia, um pintor pinta 2/5 de um muro.No dia seguinte,pinta mais 51 metros do muro.Desse modo,pintou 7/9 do muro todo.Quantos metros tem o muro?
OBS:Tenho dificuldade em interpretar o problema e assim não consigo desenvolve-lo.Sera que tem alguma regra em geral
para que eu consiga montar não só esse como outros.
*Quando montado o problema eu consigo desenvolve-lo*
-
Julie
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Ter Jul 27, 2010 00:13
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: gestão em recursos humanos
- Andamento: cursando
 por Firstlovi » Sex Jun 10, 2016 05:54
por Firstlovi » Sex Jun 10, 2016 05:54
You take the information from this place, why I could not find it.
-
Firstlovi
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sex Jun 10, 2016 05:50
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
-
Voltar para Tópicos sem Interação (leia as regras)
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Numeros racionais
por silvia fillet » Qua Out 19, 2011 20:06
- 369 Respostas
- 305132 Exibições
- Última mensagem por Estrela_36

Sáb Dez 03, 2011 17:41
Equações
-
- números: racionais
por Victor Gabriel » Dom Mai 12, 2013 14:35
- 0 Respostas
- 3220 Exibições
- Última mensagem por Victor Gabriel

Dom Mai 12, 2013 14:35
Álgebra Elementar
-
- Conjunto dos números racionais.
por scggomes » Sex Fev 18, 2011 10:38
- 4 Respostas
- 77697 Exibições
- Última mensagem por scggomes

Sex Fev 18, 2011 16:17
Álgebra Elementar
-
- Adição e Subtração de números racionais
por LuizCarlos » Sex Mar 16, 2012 20:09
- 1 Respostas
- 4888 Exibições
- Última mensagem por MarceloFantini

Sex Mar 16, 2012 22:29
Álgebra Elementar
-
- Numero irracional entre numeros racionais
por Roni Martins » Qua Fev 24, 2010 10:36
- 1 Respostas
- 11874 Exibições
- Última mensagem por Molina

Qua Fev 24, 2010 13:18
Números Complexos
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
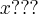 Num dia, um pintor pinta 2/5 de um muro.No dia seguinte,pinta mais 51 metros do muro.Desse modo,pintou 7/9 do muro todo.Quantos metros tem o muro?
Num dia, um pintor pinta 2/5 de um muro.No dia seguinte,pinta mais 51 metros do muro.Desse modo,pintou 7/9 do muro todo.Quantos metros tem o muro?




![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.