Dados: carga elétrica do próton=
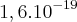C, velocidade da luz no vácuo = 300000 km/sI. A energia cinética adquirida por um próton, inicialmente em repouso e submetido à d.d.p. máxima gerada pelo LHC. é aproximadamente igual a
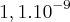J.II. Se a d.d.p. de 7x10¹² V fosse gerada por um campo elétrico uniforme de 50 kV/m, em um tubo de TV, o comprimento desse tubo seria igual a 140000 km.
III. Se a energia cinética máxima de um feixe de prótons fosse usada para acender uma lâmpada de 100 W, durante 1 s, a ordem de grandeza do número de prótons desse feixe seria igual a 10¹¹.
IV. A corrente elétrica transportada por um feixe de
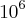prótons movendo-se dentro do acelerador circular do LHC a 90% da velocidade da luz no vácuo é igual 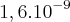a 
A.A alternativa que contém todas as afirmativas corretas é:
a) I e II
b) I e III
c) II e III
d) II e IV
e) III e IV
Tentativa de Resolução;
Se alguém puder discutir o item IV, agradeço.
Gabarito Preliminar: D
|
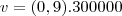
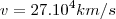
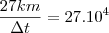
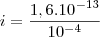
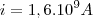
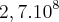
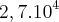
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}")
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}")
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png "{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}")
da seguinte forma:
.
da seguinte forma:
.