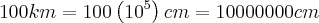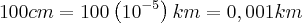por Priscila T » Sex Mar 23, 2012 17:38
Estou tentando entender o que foi passado no ensino fundamental e não consegui acompanhar.
Acredito que para transformar, por exemplo, 9,234 km em cm eu tenha que multiplicar por alguma miliagem que eu não consegui compreender. Sei que também posso simplesmente fazer a 'virgula andar' para a direita, mas eu não sei quantas casas eu deveria mexer...
-
Priscila T
- Novo Usuário
-
- Mensagens: 1
- Registrado em: Sex Mar 23, 2012 17:27
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Conversão de Unidades
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- transformar em produto
por Rhadys » Ter Jun 21, 2011 21:15
- 0 Respostas
- 1222 Exibições
- Última mensagem por Rhadys
Ter Jun 21, 2011 21:15
Trigonometria
-
- Transformar somatorio em formula
por guisantogui » Qua Mar 31, 2010 09:23
- 0 Respostas
- 3161 Exibições
- Última mensagem por guisantogui
Qua Mar 31, 2010 09:23
Progressões
-
- transformar soma em produto
por Rhadys » Ter Jun 21, 2011 15:08
- 3 Respostas
- 3170 Exibições
- Última mensagem por Claudin
Qua Jun 22, 2011 01:34
Trigonometria
-
- Transformar uma equação do 2º grau em um trinômio
por TAE » Qui Mai 24, 2012 20:29
- 1 Respostas
- 3773 Exibições
- Última mensagem por DanielFerreira
Qui Mai 24, 2012 22:06
Polinômios
-
- [Equação Plano] Transformar de geral pra paramétrica
por luankaique » Ter Ago 06, 2013 18:08
- 1 Respostas
- 4159 Exibições
- Última mensagem por Russman
Qua Ago 07, 2013 09:35
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de
Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é
Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:
Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:
Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
