A tabela abaixo apresenta uma regularidade operacional. Descubra o padrão algébrico.
Entrada -
Saída -
Resposta: Padrão algébrico = (4w/3)-1
A cada entrada corresponde uma saída, respectivamente. Os espaços com traços são para completar depois de encontrar o padrão algébrico.
Nunca vi nada desse tipo. Já fiz diversos exercícios de sequência, onde se consegue relacionar a figura com a quantidade de elementos com facilidade.
Estou há mais de 3 hs fazendo todas as tentativas possíveis. Não consegui descobrir.
Por favor, poderiam me explicar como raciocinar para descobrir esse padrão. Queria entender como montar a relação de entrada e saída.
Agradeço pela ajuda.



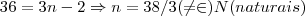 o q. aqui refutaria o problema,pois n é um natural...e assim seria com os demais,entao p/mim da forma esta o problema nao ha sol. se caso seu professor,ou alguem aqui resolve-lo poste-o pq eu gostaria de saber como resolve-lo,se tiver soluçao...
o q. aqui refutaria o problema,pois n é um natural...e assim seria com os demais,entao p/mim da forma esta o problema nao ha sol. se caso seu professor,ou alguem aqui resolve-lo poste-o pq eu gostaria de saber como resolve-lo,se tiver soluçao... saida(-,7,1,5,-11)...
saida(-,7,1,5,-11)...![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)