 por e8group » Seg Jan 20, 2014 23:45
por e8group » Seg Jan 20, 2014 23:45
Boa noite . Preciso mostrar que toda sequência periódica e convergente é constante . Por favor ,avaliem minha solução , dicas são bem vindas .
Sol.:
Dada a sequência
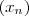
periódica e convergente ,
poremos

.Em virtude da periodicidade da sequência ,existe
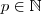
tal que
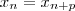
para todo

natural .Mas ,novamente por periodicidade ,temos
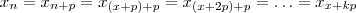
para quaisquer que seja
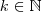
.Daí , quando

for suficientemente grande o termo
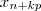
converge para

,e assim
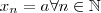
o que assegura
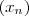
é constante.
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Sequências
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- IME-96 Função periódica
por Balanar » Sáb Ago 07, 2010 17:58
- 4 Respostas
- 10885 Exibições
- Última mensagem por kamillanjb

Ter Mar 15, 2011 22:57
Desafios Difíceis
-
- P.G. Dízima Periódica
por Rafael16 » Qua Jul 18, 2012 19:48
- 3 Respostas
- 8152 Exibições
- Última mensagem por Russman

Qua Jul 18, 2012 21:20
Progressões
-
- Dizima periodica composta
por creberson » Sex Mai 24, 2019 11:03
- 1 Respostas
- 9626 Exibições
- Última mensagem por DanielFerreira

Qui Set 12, 2019 23:19
Conjuntos
-
- [sequencia] Calcular limite de sequencia por definição
 por amigao » Ter Abr 15, 2014 15:15
por amigao » Ter Abr 15, 2014 15:15
- 4 Respostas
- 3987 Exibições
- Última mensagem por e8group

Dom Mai 11, 2014 17:09
Sequências
-
- CONVERGENTE
por camilasereno » Sáb Jun 11, 2016 20:30
- 0 Respostas
- 3651 Exibições
- Última mensagem por camilasereno

Sáb Jun 11, 2016 20:30
Conversão de Unidades
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
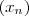 periódica e convergente ,
periódica e convergente , .Em virtude da periodicidade da sequência ,existe
.Em virtude da periodicidade da sequência ,existe 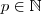 tal que
tal que 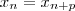 para todo
para todo  natural .Mas ,novamente por periodicidade ,temos
natural .Mas ,novamente por periodicidade ,temos 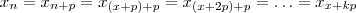 para quaisquer que seja
para quaisquer que seja 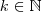 .Daí , quando
.Daí , quando  for suficientemente grande o termo
for suficientemente grande o termo 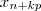 converge para
converge para  ,e assim
,e assim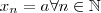 o que assegura
o que assegura 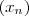 é constante.
é constante.
