 por manuoliveira » Sex Mai 23, 2014 21:07
por manuoliveira » Sex Mai 23, 2014 21:07
Não estou conseguindo resolver o exercício abaixo. Alguém poderia me explicar certinho?
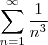
Agradeço desde já quem puder ajudar!!!
-
manuoliveira
- Usuário Parceiro

-
- Mensagens: 61
- Registrado em: Qui Abr 01, 2010 19:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Química
- Andamento: cursando
 por e8group » Sáb Mai 24, 2014 18:09
por e8group » Sáb Mai 24, 2014 18:09
manuoliveira , vc deseja verificar a convergência , não convergência dá série , só isso ? Quais ferramentas você dispõe para usar ? Podemos usar Teste da condensação de Cauchy ?
Estou dizendo isso pq , o Teste da condensação de Cauchy prova a seguinte proposição :
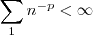
sempre que

fixo é maior que 1.
Se você interessar por outras dem. pode acessar (Está em inglês)
http://math.stackexchange.com/questions ... -for#29466ou fazer uma busca aqui no fórum .
Sem pensar no caso geral , e aceitando que

converge então pelo teste da comparação

também converge . Pq ?
Dica :

e o que acontece com a desigualdade baseada no inverso dos números ?
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Man Utd » Ter Mai 27, 2014 15:10
por Man Utd » Ter Mai 27, 2014 15:10
Boa tarde

Será que existe algum meio de achar a soma da série

??? usando a série de fourier ou qualquer outra coisa?
Neste
link o autor demonstra como achar os valores da função zeta quando

, ou seja multiplos de 2, mas não achei nada quando é ímpar.
Obrigado pela atenção.
-
Man Utd
- Colaborador Voluntário

-
- Mensagens: 155
- Registrado em: Qua Abr 03, 2013 09:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia da Computação
- Andamento: cursando
Voltar para Sequências
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Séries] Sobre simplicação de expressões em séries
por HenriqueOrlan » Sáb Nov 21, 2015 11:28
- 1 Respostas
- 3727 Exibições
- Última mensagem por adauto martins

Qua Nov 25, 2015 16:31
Sequências
-
- Séries
por Guilherme Carvalho » Seg Set 17, 2012 22:50
- 5 Respostas
- 3445 Exibições
- Última mensagem por Guilherme Carvalho

Ter Set 18, 2012 16:24
Sequências
-
- Sequencias e Séries
por Neperiano » Dom Set 26, 2010 19:28
- 1 Respostas
- 2260 Exibições
- Última mensagem por Marcampucio

Dom Set 26, 2010 21:36
Cálculo: Limites, Derivadas e Integrais
-
- Séries de pagamentos!
por Clara19 » Qua Abr 06, 2011 00:47
- 1 Respostas
- 2285 Exibições
- Última mensagem por Rogerio Murcila

Qua Mai 11, 2011 13:56
Matemática Financeira
-
- Series de Fourier
por 380625 » Qua Set 28, 2011 01:30
- 1 Respostas
- 1536 Exibições
- Última mensagem por Neperiano

Qua Set 28, 2011 15:21
Sequências
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
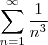

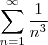

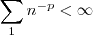 sempre que
sempre que  fixo é maior que 1.
fixo é maior que 1.  converge então pelo teste da comparação
converge então pelo teste da comparação  também converge . Pq ?
também converge . Pq ?  e o que acontece com a desigualdade baseada no inverso dos números ?
e o que acontece com a desigualdade baseada no inverso dos números ?

 ??? usando a série de fourier ou qualquer outra coisa?
??? usando a série de fourier ou qualquer outra coisa? , ou seja multiplos de 2, mas não achei nada quando é ímpar.
, ou seja multiplos de 2, mas não achei nada quando é ímpar.
