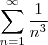
Agradeço desde já quem puder ajudar!!!

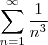

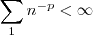 sempre que
sempre que  fixo é maior que 1.
fixo é maior que 1.  converge então pelo teste da comparação
converge então pelo teste da comparação  também converge . Pq ?
também converge . Pq ?  e o que acontece com a desigualdade baseada no inverso dos números ?
e o que acontece com a desigualdade baseada no inverso dos números ?

 ??? usando a série de fourier ou qualquer outra coisa?
??? usando a série de fourier ou qualquer outra coisa? , ou seja multiplos de 2, mas não achei nada quando é ímpar.
, ou seja multiplos de 2, mas não achei nada quando é ímpar.
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante

 .
.
 :
: