 por cardosor23 » Ter Mai 22, 2012 09:27
por cardosor23 » Ter Mai 22, 2012 09:27
Bom dia,
Relativamente à sucessão
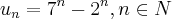
a. un coincide com a sucessão vn definida por v0 = 0, v1= 5, v2=45,
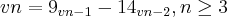
b. Cada termo un da sucessão é divisível por 5.
Tem-se que:
a. Ambas as afirmações são falsas
b. A afirmação a é verdadeira, mas a afirmação b é falsa
c. A afirmação b é verdadeira, mas a afirmação a é falsa.
d. Ambas são verdadeiras.
Abraço.
-
cardosor23
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Seg Mar 26, 2012 19:26
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Informática
- Andamento: cursando
 por fraol » Sáb Mai 26, 2012 01:29
por fraol » Sáb Mai 26, 2012 01:29
Ambas são verdadeiras.
Você pode chegar a essa conclusão usando o Princípio da Indução Finita (PIF) em ambas as alternativas assim:
Item a)
Claramente

.
Suponha que

.
Desenvolva
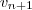
usando a definição do termo geral de
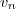
dada no enunciado e
fazendo a substituição adequada da hipótese

.
Você vai chegar em

o que mostra que

e
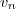
são coincidentes

.
Item b)
Use o PIF da forma convencional.
Tenta aí, qualquer coisa manda pra cá.
.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
Voltar para Sequências
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
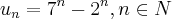
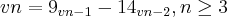


 .
. .
.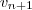 usando a definição do termo geral de
usando a definição do termo geral de 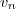 dada no enunciado e
dada no enunciado e  o que mostra que
o que mostra que  e
e  .
.