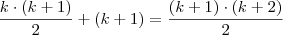por ARCS » Sáb Mar 12, 2011 01:51
por ARCS » Sáb Mar 12, 2011 01:51
Como demonstrar por indução matemática que
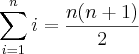
-
ARCS
- Usuário Dedicado

-
- Mensagens: 40
- Registrado em: Qui Out 28, 2010 18:55
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
 por MarceloFantini » Sáb Mar 12, 2011 02:19
por MarceloFantini » Sáb Mar 12, 2011 02:19
Você chegou a ver algum exemplo ou exercício resolvido de indução? Tem idéia de por onde começar?
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Abelardo » Sáb Mar 12, 2011 03:11
por Abelardo » Sáb Mar 12, 2011 03:11
Primeiro, tens que ''testar'' para n=1. Deves criar uma ''hipótese de indução'' com

(essa incógnita é a mais comum), por último, tens que demonstrar, algebricamente, que a fórmula
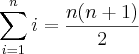
vale para

.
Como estou no ensino médio, só tive acesso a esse assunto de indução no livro 1 da coleção fundamentos da matemática elementar e no livro de aritmética de José Admo Lacerda. Existe um livrinho que trata melhor desse assunto, ''Manual de Indução Matemática - Luís Lopes'' que é muito bom para que nunca viu nada sobre o assunto.
-

Abelardo
- Colaborador Voluntário

-
- Mensagens: 159
- Registrado em: Qui Mar 03, 2011 01:45
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Renato_RJ » Sáb Mar 12, 2011 03:14
por Renato_RJ » Sáb Mar 12, 2011 03:14
Caro Arcs, essa é a soma de uma PA com elemento inicial 1 e razão 1, vejamos:

Fazemos um teste usando o menor valor possível para n, no caso o 1:

Agora façamos para n = k :
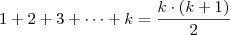
Agora façamos para n = k + 1:
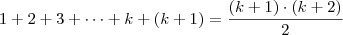
Como
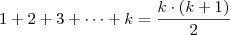
podemos fazer uma substituição no lado esquerdo da igualdade, logo teremos:
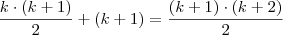
Resolvendo a soma do lado esquerdo, teremos:

Fechada a sua demonstração...
[ ]'s
Renato.
Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...
-

Renato_RJ
- Colaborador Voluntário

-
- Mensagens: 306
- Registrado em: Qui Jan 06, 2011 15:47
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado em Matemática
- Andamento: cursando
Voltar para Sequências
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Somatório
por Abelardo » Sex Abr 01, 2011 01:06
- 0 Respostas
- 1453 Exibições
- Última mensagem por Abelardo

Sex Abr 01, 2011 01:06
Álgebra Elementar
-
- Somatório
por alienante » Qua Mai 07, 2014 14:59
- 1 Respostas
- 1429 Exibições
- Última mensagem por Russman

Qua Mai 07, 2014 19:14
Álgebra Elementar
-
- Somatório e Produtório
por Abelardo » Qua Mar 23, 2011 13:49
- 1 Respostas
- 6347 Exibições
- Última mensagem por Neperiano

Dom Ago 07, 2011 22:12
Pedidos de Materiais
-
- Somatório de fatoriais
por Prof Prevaricador » Dom Abr 14, 2013 22:28
- 1 Respostas
- 2340 Exibições
- Última mensagem por marciosouza

Qua Abr 17, 2013 23:21
Sequências
-
- Somatório - limite
por livia02 » Sex Ago 16, 2013 16:31
- 1 Respostas
- 3448 Exibições
- Última mensagem por young_jedi

Sex Ago 16, 2013 19:12
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
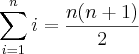




 (essa incógnita é a mais comum), por último, tens que demonstrar, algebricamente, que a fórmula
(essa incógnita é a mais comum), por último, tens que demonstrar, algebricamente, que a fórmula 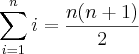 vale para
vale para  .
. 


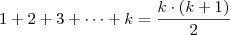
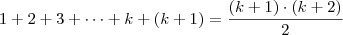
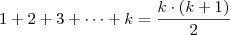 podemos fazer uma substituição no lado esquerdo da igualdade, logo teremos:
podemos fazer uma substituição no lado esquerdo da igualdade, logo teremos: