Segue o exemplo:
Seja f uma função ímpar e contínua em [-r,r], r > 0. Mostre que:
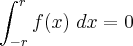
Solução:
f ímpar <-> f(-x) = -f(x) em [-r,r].
Façamos a mudança de variável u = -x
u = - x; du = - dx
x = - r; u = r
x = r; u = - r

Como f(- u) = - f(u), resulta
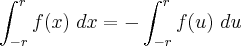 (<--- até aqui tudo bem)
(<--- até aqui tudo bem)mas,
 (veja observação acima), logo: (<--- não entendi isso)
(veja observação acima), logo: (<--- não entendi isso)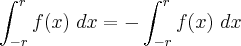
(...)
Guidorizzi, p. 322, vol. 1, 5 ed.
Estou entendo até chegar a linha que marquei. Depois não consigo entender como ele concluiu a igualdade... e como assim "veja observação acima"? Para mim ficou confuso.
Alguém pode me ajudar?


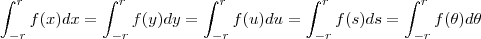

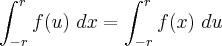
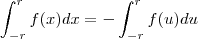
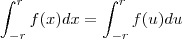



 .
.
 :
: