 por LAZAROTTI » Dom Set 30, 2012 20:29
por LAZAROTTI » Dom Set 30, 2012 20:29
Boa noite!
Alguém pode me dizer se a resposta está correta?
Atividade
Fisicamente é possível se definir a velocidade de
uma partícula pela taxa de variação da sua posição (s) em relação ao tempo, ou
seja, v=
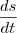
. Considere uma partícula cuja posição inicial seja 8m e se mova
com velocidade dada em m/s pela função v=
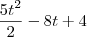
. Determine a posição da partícula quando t= 5s.
S =
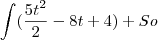
S =
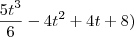
S(5) =
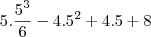
S(5) =
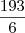
S(5) = 32,17m
Está correto?
-
LAZAROTTI
- Usuário Ativo

-
- Mensagens: 22
- Registrado em: Ter Mai 01, 2012 13:47
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
 por Russman » Dom Set 30, 2012 21:15
por Russman » Dom Set 30, 2012 21:15
A integração está correta!
Mas, por que "+8" ?
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por MarceloFantini » Seg Out 01, 2012 09:19
por MarceloFantini » Seg Out 01, 2012 09:19
Acredito que seja por isso:
Considere uma partícula cuja posição inicial seja 8m...
Ele pulou alguns passos. Note que o que aconteceu é
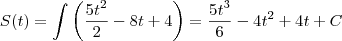
. Substituindo o valor de contorno, temos
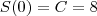
.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Integral] Duvida, pois a resposta não coincide.
por fabriel » Seg Out 29, 2012 15:26
- 2 Respostas
- 1202 Exibições
- Última mensagem por fabriel

Ter Out 30, 2012 01:48
Cálculo: Limites, Derivadas e Integrais
-
- a sua resposta!!
por weverton » Seg Jul 12, 2010 18:44
- 1 Respostas
- 1374 Exibições
- Última mensagem por weverton

Seg Jul 12, 2010 19:22
Progressões
-
- Nao comsegui axa a resposta ...
por jean » Sáb Nov 29, 2008 17:44
- 2 Respostas
- 2025 Exibições
- Última mensagem por jean

Sáb Nov 29, 2008 21:45
Pedidos
-
- Discordância de resposta
por timoteo » Qua Abr 10, 2013 13:02
- 3 Respostas
- 2742 Exibições
- Última mensagem por DanielFerreira

Ter Abr 16, 2013 21:22
Estatística
-
- resposta urgente
por vinicius gouveia » Seg Dez 23, 2013 22:17
- 1 Respostas
- 1473 Exibições
- Última mensagem por young_jedi

Seg Dez 23, 2013 23:09
Conjuntos
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
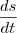 . Considere uma partícula cuja posição inicial seja 8m e se mova
. Considere uma partícula cuja posição inicial seja 8m e se mova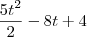
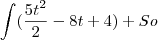
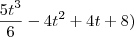
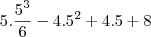
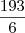



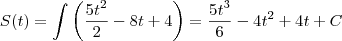 . Substituindo o valor de contorno, temos
. Substituindo o valor de contorno, temos 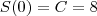 .
.
