Capítulo 3.7 - Exercício 11
Encontre a solução geral. g(t) é uma função contínua arbitrária
y11 - 5y' + 6y = g(t)
Buscando as soluções linearmente independentes da equação homogênea associada, temos

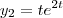
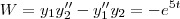
Em seguida,


O próximo passo seria calcular a integral de
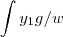 e
e 
Mas eu não sei o que fazer com essa função g que é indeterminada.
Como prosseguir?


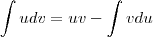
 , v =
, v = 
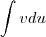 me leva para outra integral com g(t) que é o meu problema inicial.
me leva para outra integral com g(t) que é o meu problema inicial.![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)