 por inoj123 » Ter Jun 05, 2012 15:21
por inoj123 » Ter Jun 05, 2012 15:21
Boa tarde, sou novo neste fórum, por isso peço desculpa de estou a fazer algo de errado,
passo a especificar o exercício:

a solução desse limite, supostamente é -1, no entanto tentei ver o limite para algumas rectas...
para y=0, deu me uma indeterminação

para y=
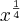
e o resultado deu me 0, visto que a solução supostamente é -1 como deveria ter encarado este exercício?
Cumprimentos,
Jóni Silva.
-
inoj123
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Ter Jun 05, 2012 15:11
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Engª Informática
- Andamento: cursando
 por LuizAquino » Qua Jun 06, 2012 10:09
por LuizAquino » Qua Jun 06, 2012 10:09
inoj123 escreveu:passo a especificar o exercício:

a solução desse limite, supostamente é -1, no entanto tentei ver o limite para algumas rectas...
para y=0, deu me uma indeterminação

para y=
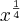
e o resultado deu me 0, visto que a solução supostamente é -1 como deveria ter encarado este exercício?
Você cometeu algum engano em suas contas.
Eu presumo que você deseja calcular o limite:

Considerando o caminho

, quando
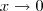
temos que
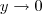
. Sendo assim, podemos reescrever o limite como sendo:



Fazendo a substituição

, quando
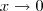
temos que

.
Além disso, temos que

. Desse modo, temos que:
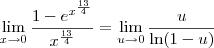
![= \lim_{u\to 0} \frac{u:u}{[\ln(1-u)]:u} = \lim_{u\to 0} \frac{u:u}{[\ln(1-u)]:u}](/latexrender/pictures/1d45fad001d1ca5b0ab7c43231d13e08.png)
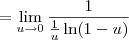

Lembrando que

, podemos obter que:
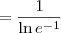
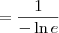
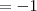
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por inoj123 » Qua Jun 06, 2012 16:03
por inoj123 » Qua Jun 06, 2012 16:03
muito obrigado! ajudou bastante
Cumprimentos,
Jóni Silva.
-
inoj123
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Ter Jun 05, 2012 15:11
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Engª Informática
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Limites] Dúvida exercício
por dehcalegari » Sex Abr 12, 2013 16:25
- 2 Respostas
- 1251 Exibições
- Última mensagem por dehcalegari

Sex Abr 12, 2013 17:06
Cálculo: Limites, Derivadas e Integrais
-
- [LIMITES] Dúvida em exercício
por Elvis » Qui Jun 18, 2015 12:03
- 1 Respostas
- 1938 Exibições
- Última mensagem por adauto martins

Sáb Jun 20, 2015 20:50
Cálculo: Limites, Derivadas e Integrais
-
- [Limites] Dúvida para terminar exercício
por dehcalegari » Seg Abr 22, 2013 15:10
- 0 Respostas
- 7158 Exibições
- Última mensagem por dehcalegari

Seg Abr 22, 2013 15:10
Cálculo: Limites, Derivadas e Integrais
-
- [limites] exercicio de calculo envolvendo limites
por lucasdemirand » Qua Jul 10, 2013 00:45
- 1 Respostas
- 4802 Exibições
- Última mensagem por e8group

Sáb Jul 20, 2013 13:08
Cálculo: Limites, Derivadas e Integrais
-
- [Limites] exercicio limites envolvendo ln
por lucasdemirand » Qua Jul 10, 2013 00:31
- 1 Respostas
- 2235 Exibições
- Última mensagem por young_jedi

Qua Jul 10, 2013 21:48
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


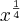 e o resultado deu me 0, visto que a solução supostamente é -1 como deveria ter encarado este exercício?
e o resultado deu me 0, visto que a solução supostamente é -1 como deveria ter encarado este exercício?


 , quando
, quando 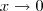 temos que
temos que 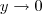 . Sendo assim, podemos reescrever o limite como sendo:
. Sendo assim, podemos reescrever o limite como sendo:


 , quando
, quando  .
. . Desse modo, temos que:
. Desse modo, temos que: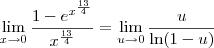
![= \lim_{u\to 0} \frac{u:u}{[\ln(1-u)]:u} = \lim_{u\to 0} \frac{u:u}{[\ln(1-u)]:u}](/latexrender/pictures/1d45fad001d1ca5b0ab7c43231d13e08.png)
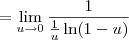

 , podemos obter que:
, podemos obter que: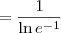
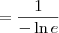
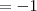

 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
