 por lo4dd » Ter Mai 22, 2012 12:08
por lo4dd » Ter Mai 22, 2012 12:08
Encontrei dificuldades de iniciar e consequentemente solucionar ( encontrar o limite ) dessa função :
Calcular o limite de

quando
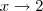
de:
![f(x)=\frac {\sqrt[3]{x} - \sqrt[3]{2}}{x - 2} f(x)=\frac {\sqrt[3]{x} - \sqrt[3]{2}}{x - 2}](/latexrender/pictures/bdc4d36061c092e195be030223e6301f.png)
Resposta :
![\frac {1}{3} \sqrt[3]{4} \frac {1}{3} \sqrt[3]{4}](/latexrender/pictures/5f4820dfbea938804656bdc7fb1274b7.png)
ou
![\frac {\sqrt[3]4} {3} \frac {\sqrt[3]4} {3}](/latexrender/pictures/1754945835f904a8968b08a1b1e2cbf2.png)
-
lo4dd
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Ter Mai 22, 2012 11:47
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. de Energias Renováveis
- Andamento: cursando
 por Thyago Quimica » Ter Mai 22, 2012 15:38
por Thyago Quimica » Ter Mai 22, 2012 15:38
-
Thyago Quimica
- Usuário Ativo

-
- Mensagens: 16
- Registrado em: Sáb Mai 05, 2012 17:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Química
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [limites] reciso de ajuda nessa questão de limites raiz quad
por alexia » Ter Nov 15, 2011 19:55
- 1 Respostas
- 5408 Exibições
- Última mensagem por LuizAquino

Qua Nov 16, 2011 15:16
Cálculo: Limites, Derivadas e Integrais
-
- [Limites]Preciso de ajuda para calcular alguns limites
por Pessoa Estranha » Ter Jul 16, 2013 17:15
- 2 Respostas
- 4754 Exibições
- Última mensagem por LuizAquino

Qua Jul 17, 2013 09:12
Cálculo: Limites, Derivadas e Integrais
-
- [Limites] Ajuda com limites no infinito e continuidade
 por umbrorz » Dom Abr 15, 2012 00:54
por umbrorz » Dom Abr 15, 2012 00:54
- 3 Respostas
- 4782 Exibições
- Última mensagem por umbrorz

Seg Abr 16, 2012 11:46
Cálculo: Limites, Derivadas e Integrais
-
- [limites] exercicio de calculo envolvendo limites
por lucasdemirand » Qua Jul 10, 2013 00:45
- 1 Respostas
- 4808 Exibições
- Última mensagem por e8group

Sáb Jul 20, 2013 13:08
Cálculo: Limites, Derivadas e Integrais
-
- [Limites] Dúvida sobre limites laterais
por Subnik » Sáb Abr 04, 2015 18:24
- 1 Respostas
- 2792 Exibições
- Última mensagem por DanielFerreira

Dom Abr 12, 2015 16:10
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 quando
quando 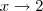 de:
de:![f(x)=\frac {\sqrt[3]{x} - \sqrt[3]{2}}{x - 2} f(x)=\frac {\sqrt[3]{x} - \sqrt[3]{2}}{x - 2}](/latexrender/pictures/bdc4d36061c092e195be030223e6301f.png)
![\frac {1}{3} \sqrt[3]{4} \frac {1}{3} \sqrt[3]{4}](/latexrender/pictures/5f4820dfbea938804656bdc7fb1274b7.png) ou
ou ![\frac {\sqrt[3]4} {3} \frac {\sqrt[3]4} {3}](/latexrender/pictures/1754945835f904a8968b08a1b1e2cbf2.png)

 quando
quando 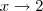 de:
de:![f(x)=\frac {\sqrt[3]{x} - \sqrt[3]{2}}{x - 2} f(x)=\frac {\sqrt[3]{x} - \sqrt[3]{2}}{x - 2}](/latexrender/pictures/bdc4d36061c092e195be030223e6301f.png)
![\frac {1}{3} \sqrt[3]{4} \frac {1}{3} \sqrt[3]{4}](/latexrender/pictures/5f4820dfbea938804656bdc7fb1274b7.png) ou
ou ![\frac {\sqrt[3]4} {3} \frac {\sqrt[3]4} {3}](/latexrender/pictures/1754945835f904a8968b08a1b1e2cbf2.png)


![\frac{\sqrt[3]{x}-\sqrt[3]{2}}{x-2}\,.\,\frac{\sqrt[3]{{x}^{2}}+\sqrt[3]{x}\sqrt[3]{2}+\sqrt[3]{{2}^{2}}}{\sqrt[3]{{x}^{2}}+\sqrt[3]{x\sqrt[3]{2}}+\sqrt[3]{{2}^{2}}} \frac{\sqrt[3]{x}-\sqrt[3]{2}}{x-2}\,.\,\frac{\sqrt[3]{{x}^{2}}+\sqrt[3]{x}\sqrt[3]{2}+\sqrt[3]{{2}^{2}}}{\sqrt[3]{{x}^{2}}+\sqrt[3]{x\sqrt[3]{2}}+\sqrt[3]{{2}^{2}}}](/latexrender/pictures/4c414b508513ec2d5d2040d1b9048793.png)
![\frac{\sqrt[3]{{x}^{3}}-\sqrt[3]{{2}^{3}}}{\left(x-2 \right){\sqrt[3]{{x}^{2}}+\sqrt[3]{x\sqrt[3]{2}}+\sqrt[3]{{2}^{2}}}} \frac{\sqrt[3]{{x}^{3}}-\sqrt[3]{{2}^{3}}}{\left(x-2 \right){\sqrt[3]{{x}^{2}}+\sqrt[3]{x\sqrt[3]{2}}+\sqrt[3]{{2}^{2}}}}](/latexrender/pictures/9d17d222bbd799f79e16541b58e6d6c4.png)
![\frac{1}{{\sqrt[3]{{x}^{2}}+\sqrt[3]{x\sqrt[3]{2}}+\sqrt[3]{{2}^{2}}}} \frac{1}{{\sqrt[3]{{x}^{2}}+\sqrt[3]{x\sqrt[3]{2}}+\sqrt[3]{{2}^{2}}}}](/latexrender/pictures/bceca6dfa2169848ac80b58983d860bc.png)
![\frac{1}{{\sqrt[3]{{2}^{2}}+\sqrt[3]{2\sqrt[3]{2}}+\sqrt[3]{{2}^{2}}}} \frac{1}{{\sqrt[3]{{2}^{2}}+\sqrt[3]{2\sqrt[3]{2}}+\sqrt[3]{{2}^{2}}}}](/latexrender/pictures/ca6b8792f456a5ebdb4986e59fd9691c.png)
![\frac{1}{\sqrt[3]{4}+\sqrt[3]{4}+\sqrt[3]{4}} \frac{1}{\sqrt[3]{4}+\sqrt[3]{4}+\sqrt[3]{4}}](/latexrender/pictures/20a293c61f391eb1dd1538f0aadf183e.png)
![= \frac{1}{3\sqrt[3]{4}} = \frac{1}{3\sqrt[3]{4}}](/latexrender/pictures/97ef03d7bcf158ff38af69035e5618e8.png)
