mostre se é divergente ou convergente!
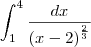
o calculo é de suma importancia.. pois nao estou conseguindo desenvolver.. caso complique para mostrar o calculo.. o que puder detalhar.. eu fico muito grato
abraço a todos

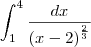

gabrielnandi escreveu:Amigos...gostaria da ajuda de voces
mostre se é divergente ou convergente!
o calculo é de suma importancia.. pois nao estou conseguindo desenvolver.. caso complique para mostrar o calculo.. o que puder detalhar.. eu fico muito grato
integrate 1/((x-2)^(2/3)) dx![\int \frac{1}{(x-2)^\frac{2}{3}} \, dx = 3\sqrt[3]{x - 2} + c \int \frac{1}{(x-2)^\frac{2}{3}} \, dx = 3\sqrt[3]{x - 2} + c](/latexrender/pictures/69227e753f43cb5827f9affe0b1dc09b.png)

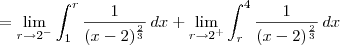
![= \lim_{r\to 2^-} \left[3\sqrt[3]{x - 2}\right]_1^r + \lim_{r\to 2^+} \left[3\sqrt[3]{x - 2}\right]_r^4 = \lim_{r\to 2^-} \left[3\sqrt[3]{x - 2}\right]_1^r + \lim_{r\to 2^+} \left[3\sqrt[3]{x - 2}\right]_r^4](/latexrender/pictures/e1c97071355ffc2a5f7e22f4cf7e8905.png)
![= \lim_{r\to 2^-} \left[3\sqrt[3]{r - 2} - 3\sqrt[3]{1 - 2}\right] + \lim_{r\to 2^+} \left[3\sqrt[3]{4 - 2} - 3\sqrt[3]{r - 2}\right] = \lim_{r\to 2^-} \left[3\sqrt[3]{r - 2} - 3\sqrt[3]{1 - 2}\right] + \lim_{r\to 2^+} \left[3\sqrt[3]{4 - 2} - 3\sqrt[3]{r - 2}\right]](/latexrender/pictures/a8e1581ac51dc06e5b94615d57f976a9.png)
![= \lim_{r\to 2^-} \left[3\sqrt[3]{r - 2} + 3\right] + \lim_{r\to 2^+} \left[3\sqrt[3]{2} - 3\sqrt[3]{r - 2}\right] = \lim_{r\to 2^-} \left[3\sqrt[3]{r - 2} + 3\right] + \lim_{r\to 2^+} \left[3\sqrt[3]{2} - 3\sqrt[3]{r - 2}\right]](/latexrender/pictures/0110a5df603af86c09a094d373d94338.png)
![= 3 + 3\sqrt[3]{2} = 3 + 3\sqrt[3]{2}](/latexrender/pictures/80829112343e0197ce9a94493df70d80.png)

Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes

 .
.
 :
: