Como calcular por definição o seguinte limite:
lim (3x² -7x + 2) = -2, quando x tende a 1; EPSILON = 0,02




Russman escreveu:Só substituir x=1 na função !
f(x) = 3x² - 7x + 2
f(1) = 3-7+2 = -2

felipe10 escreveu:Como calcular por definição o seguinte limite:
lim (3x² -7x + 2) = -2, quando x tende a 1; EPSILON = 0,02
 tal que:
tal que: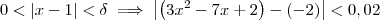
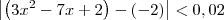

 , temos que
, temos que  .
.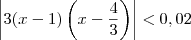

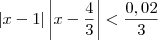
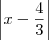 . Como x se aproxima de 1, é razoável dizer que x está no intervalo
. Como x se aproxima de 1, é razoável dizer que x está no intervalo 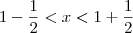 (ou seja,
(ou seja, 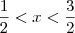 ). Analisando agora o gráfico da função
). Analisando agora o gráfico da função  para x no intervalo
para x no intervalo 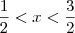 , temos que
, temos que  . Vide a figura abaixo.
. Vide a figura abaixo.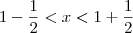 , estamos dizendo que
, estamos dizendo que 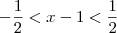 . Ou seja, estamos dizendo que
. Ou seja, estamos dizendo que 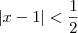 . Isso significa que estamos escolhendo um certo
. Isso significa que estamos escolhendo um certo 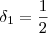 .
. , temos que:
, temos que: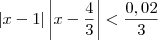


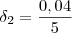 .
. . Mas qual deles devemos usar? Devemos usar aquele que garanta ao mesmo tempo que duas coisas aconteçam:
. Mas qual deles devemos usar? Devemos usar aquele que garanta ao mesmo tempo que duas coisas aconteçam: ;
; .
.  como sendo o menor dos dois valores. Isto é, escolheremos
como sendo o menor dos dois valores. Isto é, escolheremos  . Como
. Como  nesse caso, vamos escolher
nesse caso, vamos escolher  .
.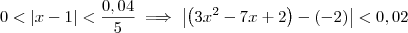
 realmente funciona.
realmente funciona.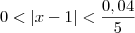 , podemos afirmar que
, podemos afirmar que 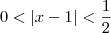 . Podemos afirmar isso, pois 0,04/5 = 0,008 e 1/2 = 0,5. Sendo assim, se |x - 1| é um número menor do que 0,008, então ele também será menor do que 0,5. Por outro lado, como já vimos anteriormente, se
. Podemos afirmar isso, pois 0,04/5 = 0,008 e 1/2 = 0,5. Sendo assim, se |x - 1| é um número menor do que 0,008, então ele também será menor do que 0,5. Por outro lado, como já vimos anteriormente, se 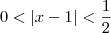 , então
, então  . Resumindo, temos que:
. Resumindo, temos que:

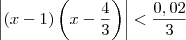



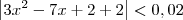
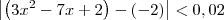
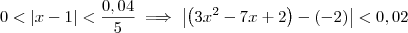

Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes


 substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.