f(x)= sen(x)+cos(3x) ,
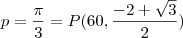 ------------- f(p)=
------------- f(p)=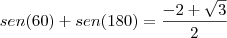
Resolvendo:

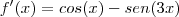
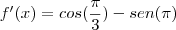
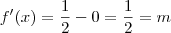
Para determinar a equação:

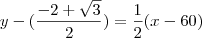

Mas testando pelo Geogebra, o resultado da equação da reta tangente em (p,f(p)) é:

Que consigo obter quando coloco o ponto P = (
 , onde
, onde 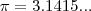 Então devo usar o pi = 180 da trigononometria, ou a constante pi = 3,1415... em questões desse tipo??? Espero que entendam o q escrevi, Agradeço qualquer ajuda.
Então devo usar o pi = 180 da trigononometria, ou a constante pi = 3,1415... em questões desse tipo??? Espero que entendam o q escrevi, Agradeço qualquer ajuda.

 como 180º quando aplicas diretamente em funções trigonométricas, ou seja, nos cálculos de sen, cos, tg, cotg, .... Portanto quanto calculas f(
como 180º quando aplicas diretamente em funções trigonométricas, ou seja, nos cálculos de sen, cos, tg, cotg, .... Portanto quanto calculas f( ), vais calcular o sen e cos de
), vais calcular o sen e cos de 
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
