 por Cleyson007 » Sáb Abr 14, 2012 10:07
por Cleyson007 » Sáb Abr 14, 2012 10:07
Bom dia a todos!
Calcule a integral iterada

e esboce sua região de integração.
Calculando a integral iterada encontrei
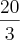
e fiz o esboço da área de integração. Segue o esboço para avaliação:

Aguardo retorno.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por LuizAquino » Sáb Abr 14, 2012 11:43
por LuizAquino » Sáb Abr 14, 2012 11:43
Cleyson007 escreveu:Calcule a integral iterada

e esboce sua região de integração.
Calculando a integral iterada encontrei
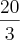
e fiz o esboço da área de integração.
DicaPara conferir a sua reposta, você pode usar um programa. Por exemplo, o
SAGE, o Mathematica, o Maple, etc.
Alguns desses programas são disponibilizados também na forma de uma página na internet. É o caso do
SAGE Notebook e do Mathematica. Por exemplo, siga os passos abaixo para conferir a sua resolução.
- Acesse a página: http://www.wolframalpha.com/
- No campo de entrada, digite:
- Código: Selecionar todos
integrate (integrate 2x + 4y dy from x to 3x) dx from 0 to 1
- Clique no botão de igual ao lado do campo de entrada.
- Pronto! Agora basta comparar o resultado com o seu.
Cleyson007 escreveu: Segue o esboço para avaliação:
O gráfico da reta y = 3x está errado. Note que essa reta deve passar, por exemplo, nos pontos (0, 0) e (1, 3).
Tente refazer o esboço.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Cleyson007 » Dom Abr 15, 2012 10:09
por Cleyson007 » Dom Abr 15, 2012 10:09
Bom dia Luiz Aquino!
Refiz o esboço da região e usei o programa apenas para conferir.
Nossa, não sei de onde tinha tirado a reta y=3x rsrsrs
Segue novo esboço:

Aquino, brigado pela ajuda.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Região de integração e esboço
 por Cleyson007 » Sáb Abr 14, 2012 10:57
por Cleyson007 » Sáb Abr 14, 2012 10:57
- 5 Respostas
- 5758 Exibições
- Última mensagem por DanielFerreira

Dom Abr 15, 2012 19:45
Cálculo: Limites, Derivadas e Integrais
-
- Esboço da região de integração - coordenadas cilíndricas
por BrunoCPL » Dom Set 09, 2018 17:48
- 1 Respostas
- 6073 Exibições
- Última mensagem por Gebe

Seg Set 10, 2018 11:00
Cálculo: Limites, Derivadas e Integrais
-
- Região de integração
por Cleyson007 » Sex Abr 13, 2012 23:00
- 5 Respostas
- 2457 Exibições
- Última mensagem por DanielFerreira

Sáb Abr 14, 2012 00:19
Cálculo: Limites, Derivadas e Integrais
-
- Região de integração
por Cleyson007 » Qua Abr 18, 2012 11:43
- 1 Respostas
- 1388 Exibições
- Última mensagem por LuizAquino

Qui Abr 19, 2012 14:20
Cálculo: Limites, Derivadas e Integrais
-
- Região de integração
 por Cleyson007 » Qua Abr 18, 2012 16:47
por Cleyson007 » Qua Abr 18, 2012 16:47
- 3 Respostas
- 1604 Exibições
- Última mensagem por DanielFerreira

Sáb Abr 21, 2012 14:47
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 9 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 e esboce sua região de integração.
e esboce sua região de integração.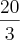 e fiz o esboço da área de integração. Segue o esboço para avaliação:
e fiz o esboço da área de integração. Segue o esboço para avaliação:

 e esboce sua região de integração.
e esboce sua região de integração.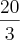 e fiz o esboço da área de integração. Segue o esboço para avaliação:
e fiz o esboço da área de integração. Segue o esboço para avaliação:

e esboce sua região de integração.
e fiz o esboço da área de integração.



 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.