souzalucasr escreveu:Calcule o limite a seguir:
![\lim_{x\rightarrow0}\frac{\sqrt[3]{x}-1}{x^2-x} \lim_{x\rightarrow0}\frac{\sqrt[3]{x}-1}{x^2-x}](/latexrender/pictures/ca45b28898898b7f78ed8763982cd50b.png)
souzalucasr escreveu:Utilizei a equivalência

, de forma a obter
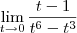
=
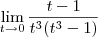
=
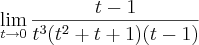
cancelando os termos

no denominador e numerador, obtive

Foi exatamente nesse ponto em que "travei". Ao entregar a prova, perguntei ao professor como poderia resolver e ele me disse que seria pela análise do sinal, mas não sei bem o que isso quer dizer e como fazer. Vocês poderiam me ajudar?
A dica sobre a "análise do sinal" é devido ao fato desse limite ter como resultado

.
Como já disse o colega
MarceloFantini, analisando a expressão original do limite, note que o numerador tende para -1 e o denominador para 0. Isso já é um indício que temos um limite cujo o resultado é

. Falta agora saber se é

ou

. Para saber disso precisamos analisar o sinal.
Para x próximo de 0, temos que o numerador é negativo (como já vimos, ele tende para -1).
Precisamos agora analisar o sinal do denominador quando x está próximo de 0. Isso significa que precisamos analisar o sinal da função
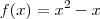
quando x está próximo de zero. Fazendo o estudo do sinal dessa função polinomial do segundo grau, percebemos que f(x) tende para 0 por valores positivos, quando x tende a 0 pela esquerda. Por outro lado, f(x) tende para 0 por valores negativos, quando x tende a 0 pela direita.
Em resumo:
(i) quando x tende a 0 pela esquerda, o numerador é negativo e o denominador é positivo;
(ii) quando x tende a 0 pela direita, o numerador é negativo e o denominador é negativo;
Conclusão:
![\lim_{x\to 0^-} \frac{\sqrt[3]{x} - 1}{x^2 - x} = -\infty \lim_{x\to 0^-} \frac{\sqrt[3]{x} - 1}{x^2 - x} = -\infty](/latexrender/pictures/cd763d09f9c46589bb78e54b5bf3d3db.png)
![\lim_{x\to 0^+} \frac{\sqrt[3]{x} - 1}{x^2 - x} = +\infty \lim_{x\to 0^+} \frac{\sqrt[3]{x} - 1}{x^2 - x} = +\infty](/latexrender/pictures/ca23a7c9df3111da51374883cda55923.png)
Como esses limites laterais são diferentes, temos que
não existe o limite
![\lim_{x\to 0} \frac{\sqrt[3]{x} - 1}{x^2 - x} \lim_{x\to 0} \frac{\sqrt[3]{x} - 1}{x^2 - x}](/latexrender/pictures/ea17b159bfcabc8a50c0338778963f42.png)
.
souzalucasr escreveu:Eu não estou com a prova em mãos, mas tenho 99% de certeza que é x tendendo a 0, pois houve esse comentário do professor quanto ao "estudo do sinal". Eu faltei a essa aula, por isso estou perdido. Além disso, não encontrei nada no livro.
Eu gostaria de recomendar que você assista a videoaula "05. Cálculo I - Limites Infinitos". Ela está disponível em meu canal no YouTube:
http://www.youtube.com/LCMAquino![\lim_{x\rightarrow0}\frac{\sqrt[3]{x}-1}{x^2-x} \lim_{x\rightarrow0}\frac{\sqrt[3]{x}-1}{x^2-x}](/latexrender/pictures/ca45b28898898b7f78ed8763982cd50b.png)
 , de forma a obter
, de forma a obter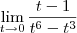 =
= 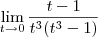 =
= 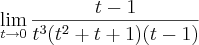
 no denominador e numerador, obtive
no denominador e numerador, obtive 


 mesmo? Se já viram limites infinitos, a resposta sai de cara da primeira linha, pois o numerador tende a menos um e o denominador para zero.
mesmo? Se já viram limites infinitos, a resposta sai de cara da primeira linha, pois o numerador tende a menos um e o denominador para zero.

 .
. ou
ou  . Para saber disso precisamos analisar o sinal.
. Para saber disso precisamos analisar o sinal.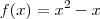 quando x está próximo de zero. Fazendo o estudo do sinal dessa função polinomial do segundo grau, percebemos que f(x) tende para 0 por valores positivos, quando x tende a 0 pela esquerda. Por outro lado, f(x) tende para 0 por valores negativos, quando x tende a 0 pela direita.
quando x está próximo de zero. Fazendo o estudo do sinal dessa função polinomial do segundo grau, percebemos que f(x) tende para 0 por valores positivos, quando x tende a 0 pela esquerda. Por outro lado, f(x) tende para 0 por valores negativos, quando x tende a 0 pela direita.![\lim_{x\to 0^-} \frac{\sqrt[3]{x} - 1}{x^2 - x} = -\infty \lim_{x\to 0^-} \frac{\sqrt[3]{x} - 1}{x^2 - x} = -\infty](/latexrender/pictures/cd763d09f9c46589bb78e54b5bf3d3db.png)
![\lim_{x\to 0^+} \frac{\sqrt[3]{x} - 1}{x^2 - x} = +\infty \lim_{x\to 0^+} \frac{\sqrt[3]{x} - 1}{x^2 - x} = +\infty](/latexrender/pictures/ca23a7c9df3111da51374883cda55923.png)
![\lim_{x\to 0} \frac{\sqrt[3]{x} - 1}{x^2 - x} \lim_{x\to 0} \frac{\sqrt[3]{x} - 1}{x^2 - x}](/latexrender/pictures/ea17b159bfcabc8a50c0338778963f42.png) .
.