 valha.
valha.Dê então um valor pra
 >0 tal que para todo x satisfazendo 0<|x-a|<
>0 tal que para todo x satisfazendo 0<|x-a|< a desigualdade |f(x)-L|<seja verdadeira.
a desigualdade |f(x)-L|<seja verdadeira.f(x)=
 , L=3, a=10,
, L=3, a=10,  =1
=1o intervalo eu conseguir achar, da seguinte maneira:
0<|x-10|<

 |
| -3|<1
-3|<13-1<|
 <4
<42<|
 <4
<44<|19-x|<16
-15<|-x|<-3
15>|x|>3
logo (3,15) confere com a resposta do livro, acredito que a resolução esteja correta.
Mas ai, o valor de
 não consigo achar, sempre acho -7, mas no livro a resposta é 5.
não consigo achar, sempre acho -7, mas no livro a resposta é 5.Alguem poderia ajudar-me por favor?
Obg
Ps: Livro Calculo 1, Thomas, pag 92, nro 19


 dado, você encontrou
dado, você encontrou 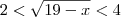 .
.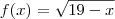 , encontramos
, encontramos  e
e 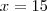 .
.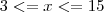 .
.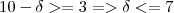 e
e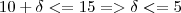
 a implicação do limite será satisfeita.
a implicação do limite será satisfeita.
 .
. e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
