 por -civil- » Sex Mar 23, 2012 18:31
por -civil- » Sex Mar 23, 2012 18:31
Estava tentando fazer a integral dupla de
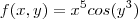
no retângulo
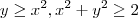
Eu não consegui resolver desenvolvendo a integral e na resolução diz apenas que a função é ímpar na variável x e o resultado da integral é zero.
Eu consigo entender que a integral da uma função ímpar centrada na origem é zero (Se ela tem a mesma simetria). Mas como eu descubro que a função
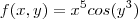
é ímpar se eu não faço a menor ideia de como é o gráfico dela? Eu vou ter que seguir todo aquele processo de esboço de gráfico?
Um outro jeito de provar que a função é ímpar é verificar se f(-x) = -f(x). No caso, como fica a fórmula para duas variáveis?
-
-civil-
- Usuário Dedicado

-
- Mensagens: 47
- Registrado em: Sex Abr 22, 2011 12:31
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
 por LuizAquino » Sex Mar 23, 2012 22:58
por LuizAquino » Sex Mar 23, 2012 22:58
-civil- escreveu:Estava tentando fazer a integral dupla de
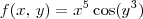
no retângulo
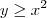
,
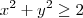
A região de integração não seria
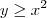
,
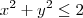
?
Além disso, note que essa região (e nem a que você escreveu antes) não é um "retângulo".
-civil- escreveu:Um outro jeito de provar que a função é ímpar é verificar se f(-x) = -f(x). No caso, como fica a fórmula para duas variáveis?
Quando ele diz que "(...) a função é ímpar na variável x (...)", ele está dizendo que f(-x, y) = -f(x, y).
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Integral] Integral funçao trigonometrica
por ewald » Qua Ago 17, 2011 22:33
- 2 Respostas
- 2843 Exibições
- Última mensagem por ewald

Qui Ago 18, 2011 00:54
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Integral funçao trigonometrica
por ewald » Sáb Ago 20, 2011 17:20
- 2 Respostas
- 2866 Exibições
- Última mensagem por LuizAquino

Dom Ago 21, 2011 21:14
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Integral funçao trigonometrica
por ewald » Seg Ago 22, 2011 00:44
- 1 Respostas
- 1428 Exibições
- Última mensagem por LuizAquino

Seg Ago 22, 2011 08:52
Cálculo: Limites, Derivadas e Integrais
-
- Função real definida pela soma de uma função par c/uma ímpar
por Taah » Sáb Mar 27, 2010 15:33
- 3 Respostas
- 5571 Exibições
- Última mensagem por Taah

Dom Mar 28, 2010 13:21
Funções
-
- funcao impar
por irineu junior » Sex Mar 12, 2010 20:49
- 2 Respostas
- 2558 Exibições
- Última mensagem por irineu junior

Dom Mar 14, 2010 20:55
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
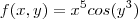 no retângulo
no retângulo 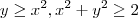
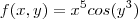 é ímpar se eu não faço a menor ideia de como é o gráfico dela? Eu vou ter que seguir todo aquele processo de esboço de gráfico?
é ímpar se eu não faço a menor ideia de como é o gráfico dela? Eu vou ter que seguir todo aquele processo de esboço de gráfico?

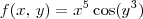 no retângulo
no retângulo 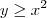 ,
, 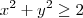
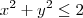 ?
?
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
