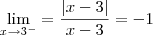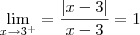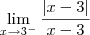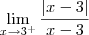por matmatco » Qui Mar 22, 2012 23:18
por matmatco » Qui Mar 22, 2012 23:18
não estou conseguindo entender como sair desse modulo

-
matmatco
- Usuário Parceiro

-
- Mensagens: 60
- Registrado em: Qua Ago 24, 2011 17:32
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matematica UFV
- Andamento: cursando
 por fraol » Qui Mar 22, 2012 23:35
por fraol » Qui Mar 22, 2012 23:35
Esse limite não existe.
Observe que o numerador é um número positivo.
Já o denominador é um número positivo se x tende a 3 pela direita
ou é um número negativo se x tende a 3 pela esquerda.
Em outras palavras, os limites laterais são diferentes.
Você saberia dizer qual é o limite quando x tende a 3 pela direita e quando x tende a 3 pela esquerda?
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por matmatco » Sex Mar 23, 2012 09:21
por matmatco » Sex Mar 23, 2012 09:21
não
-
matmatco
- Usuário Parceiro

-
- Mensagens: 60
- Registrado em: Qua Ago 24, 2011 17:32
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matematica UFV
- Andamento: cursando
 por fraol » Seg Mar 26, 2012 19:45
por fraol » Seg Mar 26, 2012 19:45
Observe:
Quando x tende a 3 pela esquerda, x < 3, x - 3 é um número negativo. Então:
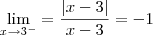
Quando x tende a 3 pela direita, x > 3, x - 3 é um número positivo. Então:
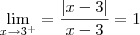
É por isso que o limite pedido não existe pois, os limites laterais são diferentes.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por matmatco » Ter Mar 27, 2012 10:08
por matmatco » Ter Mar 27, 2012 10:08
entendi..muito obrigado
abraços
-
matmatco
- Usuário Parceiro

-
- Mensagens: 60
- Registrado em: Qua Ago 24, 2011 17:32
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matematica UFV
- Andamento: cursando
 por LuizAquino » Ter Mar 27, 2012 13:01
por LuizAquino » Ter Mar 27, 2012 13:01
fraol escreveu:Observe:
Quando x tende a 3 pela esquerda, x < 3, x - 3 é um número negativo. Então:
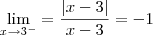
Quando x tende a 3 pela direita, x > 3, x - 3 é um número positivo. Então:
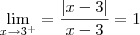
É por isso que o limite pedido não existe pois, os limites laterais são diferentes.
Apenas uma observação. A notação correta é:
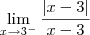
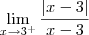
Note que na sua escrita você colocou um "=" fora do lugar.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por fraol » Ter Mar 27, 2012 13:06
por fraol » Ter Mar 27, 2012 13:06
Ok. Foi um lapso na digitação. Grato.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por LuizAquino » Ter Mar 27, 2012 13:14
por LuizAquino » Ter Mar 27, 2012 13:14
fraol escreveu:Ok. Foi um lapso na digitação. Grato.
No seu caso eu imaginei isso.
Mas sempre é bom chamar a atenção quanto a escrita matemática.
Existem muitos estudantes que cometem o mesmo equívoco de escrever esse "=" no lugar errado.
Também foi o caso de
matmatco:
matmatco escreveu:não estou conseguindo entender como sair desse modulo

-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Limite (envolvendo Módulo)
por killerkill » Ter Ago 09, 2011 23:12
- 7 Respostas
- 11104 Exibições
- Última mensagem por LuizAquino

Qua Ago 10, 2011 11:47
Cálculo: Limites, Derivadas e Integrais
-
- [integral envolvendo módulo]
por Fabio Wanderley » Sex Dez 14, 2012 11:14
- 3 Respostas
- 2695 Exibições
- Última mensagem por young_jedi

Sex Dez 14, 2012 16:04
Cálculo: Limites, Derivadas e Integrais
-
- Limite com Módulo
por Man Utd » Sex Mai 10, 2013 10:45
- 6 Respostas
- 8879 Exibições
- Última mensagem por Man Utd

Sáb Mai 11, 2013 14:29
Cálculo: Limites, Derivadas e Integrais
-
- Limite com Modulo em denominador
por orainha » Sex Fev 03, 2017 23:12
- 2 Respostas
- 8286 Exibições
- Última mensagem por orainha

Qui Mar 30, 2017 21:42
Cálculo: Limites, Derivadas e Integrais
-
- limite envolvendo exponencial
por renat » Dom Jun 11, 2017 20:37
- 0 Respostas
- 2834 Exibições
- Última mensagem por renat

Dom Jun 11, 2017 20:37
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.