 por miumatos » Dom Mar 18, 2012 13:06
por miumatos » Dom Mar 18, 2012 13:06
Bom dia pessoal, preciso de uma ajuda para entender a seguinte função:

sei que o resultado é
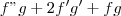
e a questão pede para provar derivando até a segunda ordem que uma é igual a outra.
já entendo como derivar com numeros mas não consegui associar com este tipo de função.
Agradeço desde já.
-
miumatos
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Dom Mar 18, 2012 12:33
- Formação Escolar: GRADUAÇÃO
- Área/Curso: sistemas de informação
- Andamento: cursando
 por LuizAquino » Dom Mar 18, 2012 13:18
por LuizAquino » Dom Mar 18, 2012 13:18
miumatos escreveu:Bom dia pessoal, preciso de uma ajuda para entender a seguinte função:

sei que o resultado é
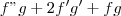
e a questão pede para provar derivando até a segunda ordem que uma é igual a outra.
já entendo como derivar com numeros mas não consegui associar com este tipo de função.
Você deseja calcular a segunda derivada do produto entre duas funções. Isto é, você deseja calcular
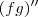
.
Efetuar esse cálculo é o mesmo que fazer
![[(fg)^{\prime}]^{\prime} [(fg)^{\prime}]^{\prime}](/latexrender/pictures/350db2a3bf8316181307de0b5b15aa20.png)
.
Aplicando a regra do produto para derivadas, temos que:
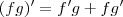
Sendo assim, temos que:
![(fg)^{\prime\prime} = [(fg)^{\prime}]^{\prime} (fg)^{\prime\prime} = [(fg)^{\prime}]^{\prime}](/latexrender/pictures/04d487b63e678689dcf7b1c6f1f7d4af.png)
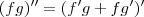
Aplicando agora a regra da soma para derivadas, temos que:
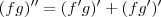
Aplicando novamente a regra do produto para derivadas, temos que:
![(fg)^{\prime\prime} = [(f^\prime)^\prime g + f^\prime g^\prime] + [f^\prime g^\prime + f (g^\prime)^\prime] (fg)^{\prime\prime} = [(f^\prime)^\prime g + f^\prime g^\prime] + [f^\prime g^\prime + f (g^\prime)^\prime]](/latexrender/pictures/100a0dd9f5de7213d4259287b4eedda0.png)

-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por miumatos » Dom Mar 18, 2012 15:29
por miumatos » Dom Mar 18, 2012 15:29

ok, entendi.
Muito obrigado.
-
miumatos
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Dom Mar 18, 2012 12:33
- Formação Escolar: GRADUAÇÃO
- Área/Curso: sistemas de informação
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Derivada simples
por vanu » Qua Dez 11, 2013 15:03
- 0 Respostas
- 1590 Exibições
- Última mensagem por vanu

Qua Dez 11, 2013 15:03
Cálculo: Limites, Derivadas e Integrais
-
- Derivada simples
por vanu » Qua Dez 11, 2013 15:19
- 1 Respostas
- 1747 Exibições
- Última mensagem por e8group

Qua Dez 11, 2013 16:11
Cálculo: Limites, Derivadas e Integrais
-
- Derivada - Duvida simples
por iceman » Ter Set 18, 2012 19:06
- 1 Respostas
- 1592 Exibições
- Última mensagem por Renato_RJ

Ter Set 18, 2012 19:20
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada] Simples cubo
por Matheus321 » Ter Out 25, 2016 21:13
- 1 Respostas
- 5449 Exibições
- Última mensagem por DanielFerreira

Sáb Nov 26, 2016 18:46
Cálculo: Limites, Derivadas e Integrais
-
- [Derivadas] Questão simples de derivada.
por Gustavo195 » Ter Mai 14, 2013 17:52
- 0 Respostas
- 1597 Exibições
- Última mensagem por Gustavo195

Ter Mai 14, 2013 17:52
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 7 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

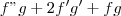 e a questão pede para provar derivando até a segunda ordem que uma é igual a outra.
e a questão pede para provar derivando até a segunda ordem que uma é igual a outra.

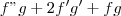 e a questão pede para provar derivando até a segunda ordem que uma é igual a outra.
e a questão pede para provar derivando até a segunda ordem que uma é igual a outra.
e a questão pede para provar derivando até a segunda ordem que uma é igual a outra.
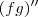 .
.![[(fg)^{\prime}]^{\prime} [(fg)^{\prime}]^{\prime}](/latexrender/pictures/350db2a3bf8316181307de0b5b15aa20.png) .
.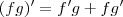
![(fg)^{\prime\prime} = [(fg)^{\prime}]^{\prime} (fg)^{\prime\prime} = [(fg)^{\prime}]^{\prime}](/latexrender/pictures/04d487b63e678689dcf7b1c6f1f7d4af.png)
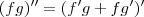
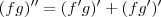
![(fg)^{\prime\prime} = [(f^\prime)^\prime g + f^\prime g^\prime] + [f^\prime g^\prime + f (g^\prime)^\prime] (fg)^{\prime\prime} = [(f^\prime)^\prime g + f^\prime g^\prime] + [f^\prime g^\prime + f (g^\prime)^\prime]](/latexrender/pictures/100a0dd9f5de7213d4259287b4eedda0.png)




