thiago toledo escreveu:Quais as dimensões do cilindro circular reto e de areá lateral máxima que pode ser inscrito numa esfera de raio R?
A figura abaixo ilustra o exercício.
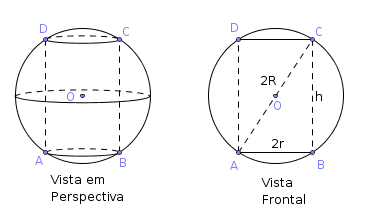
- cilindro_e_esfera.png (8.9 KiB) Exibido 756 vezes
thiago toledo escreveu:(...) eu sei que a areá lateral de um cilindro é: A=2.pi.r.h (...)
Ok.
thiago toledo escreveu:(...) e a areá da esfera é A' = 2.pi.R² (..)
Errado. A área da esfera é
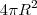
. Entretanto, não é necessário usar essa informação no exercício.
thiago toledo escreveu:(...) como eu resumo a equação para que eu possa derivar e encontrar as dimensões do cilindro, ou seja, seu raio e sua altura? (...)
Analisando a figura acima, note que:

Dessa forma, a área lateral do cilindro em função do raio r será:
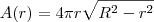
Agora tente terminar o exercício.


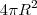 . Entretanto, não é necessário usar essa informação no exercício.
. Entretanto, não é necessário usar essa informação no exercício.
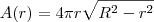

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.