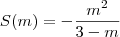Considere um triângulo retângulo no primeiro quadrante limitados pelos eixos coordenados e pela reta que passa pelo ponto P(2,3). Encontre os vértices do triangulo de areá máxima.
O exercício deveria solicitar os vértices do triângulo de área mínima. Vide figura abaixo.
thiago toledo escreveu:Como resolvo este exercício?
A figura abaixo ilustra o exercício.
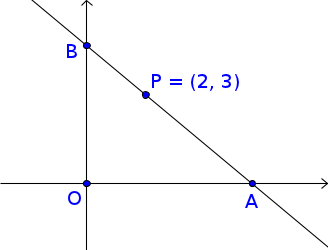
- triângulo.png (5.04 KiB) Exibido 2503 vezes
Note que uma "área máxima" ocorreria quando a reta fosse paralela ao eixo x (passando por P), o que não formaria um triângulo. Ou ainda, também ocorreria uma "área máxima" se a reta estivesse passando por OP, mas nesse o triângulo não estaria limitado.
O exercício deveria então solicitar que sejam determinados os vértices A e B de modo que OAB tenha área mínima.
Lembre-se que a reta passando por A, P e B tem o formato
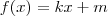
. Além disso, deve-se ter
k < 0, já que a função deve ser decrescente (como ilustra a figura).
Como P = (2, 3) pertence a reta, deve ocorrer
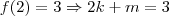
.
O ponto A tem coordenada y igual a zero. Portanto, ele deve ter o formato A = (-m/k, 0).
Por outro lado, o ponto B tem coordenada x igual a zero. Portanto, ele deve ter o formato B = (0, m).
Nessas condições, a área de OAB será dada por:
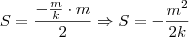
Apesar do sinal de menos aparecer na expressão para S, note que S continua sendo um número positivo, pois
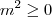
e
k < 0.
Lembrando-se que deve ocorrer
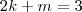
, podemos dizer que:
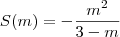
Basta agora encontrar o ponto de mínimo dessa função.
Tente concluir o exercício a partir daqui.



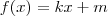 . Além disso, deve-se ter k < 0, já que a função deve ser decrescente (como ilustra a figura).
. Além disso, deve-se ter k < 0, já que a função deve ser decrescente (como ilustra a figura).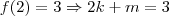 .
.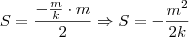
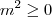 e k < 0.
e k < 0.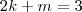 , podemos dizer que:
, podemos dizer que: