 por jr_freitas » Seg Out 31, 2011 14:02
por jr_freitas » Seg Out 31, 2011 14:02
Boa tarde!
Podem me ajudar no seguinte exercício de integral?
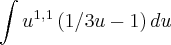
Eu consigo chegar até essa parte, depois não sei o que faço:
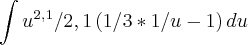
, estou fazendo errado?...por favor me expliquem!
Obrigado!
-
jr_freitas
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Qui Out 06, 2011 10:28
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Tecnólogo em Análise de Sistemas
- Andamento: cursando
 por MarceloFantini » Seg Out 31, 2011 15:05
por MarceloFantini » Seg Out 31, 2011 15:05
Freitas, não é possível entender qual é a integral a ser calculada. Para utilizar fração, use o comando
- Código: Selecionar todos
\frac{a}{b}
e o resultado será

. Para fazer um produto, use
- Código: Selecionar todos
c \cdot d
e aparecerá

.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por jr_freitas » Seg Out 31, 2011 15:49
por jr_freitas » Seg Out 31, 2011 15:49
Ok! Desculpe.
Não consigo resolver o seguinte exercício de Integral:

Eu consigo chegar até essa parte, depois não sei o que faço:

, (não sei se está certo).
Obrigado pela ajuda!
-
jr_freitas
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Qui Out 06, 2011 10:28
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Tecnólogo em Análise de Sistemas
- Andamento: cursando
 por MarceloFantini » Seg Out 31, 2011 16:07
por MarceloFantini » Seg Out 31, 2011 16:07
Se você aplicar a distributiva, verá que a integral fica

. É isso? Ainda não entendo porque apareceria um expoente fracionário.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por procyon » Ter Nov 01, 2011 00:16
por procyon » Ter Nov 01, 2011 00:16
![\int u^{1,1}. \left( \frac{1}{3u} -1 \right).du \\
\\
\text{Distribuindo os fatores:} \\
\\
\int \left[ u^{1,1}. \frac{1}{3u} -1 . u^{1,1} \right]du\\
\\
\text{Distribuindo as potencias:} \\
\\
\int \left[ \frac{u^{1}.u^{0,1}}{3u} -1 . u^{1,1} \right]du \\
\\
\text{Cortando o que puder e usando a propriedade da diferenca de uma integral:} \\
\\
\frac{1}{3} \int u^{0,1}.du - \int u^{1,1}du \\
\\
\text{Integrando temos:} \\
\\
\left[ \frac{1}{3} . \frac{u^{1,1}}{1,1} - \frac{u^{2,1}}{2,1} \right] + C \\
\\
\text{E finalmente:} \\
\\
\frac{u^{1,1}}{3,3} - \frac{u^{2,1}}{2,1} + C \int u^{1,1}. \left( \frac{1}{3u} -1 \right).du \\
\\
\text{Distribuindo os fatores:} \\
\\
\int \left[ u^{1,1}. \frac{1}{3u} -1 . u^{1,1} \right]du\\
\\
\text{Distribuindo as potencias:} \\
\\
\int \left[ \frac{u^{1}.u^{0,1}}{3u} -1 . u^{1,1} \right]du \\
\\
\text{Cortando o que puder e usando a propriedade da diferenca de uma integral:} \\
\\
\frac{1}{3} \int u^{0,1}.du - \int u^{1,1}du \\
\\
\text{Integrando temos:} \\
\\
\left[ \frac{1}{3} . \frac{u^{1,1}}{1,1} - \frac{u^{2,1}}{2,1} \right] + C \\
\\
\text{E finalmente:} \\
\\
\frac{u^{1,1}}{3,3} - \frac{u^{2,1}}{2,1} + C](/latexrender/pictures/40b37199df4fdb2befd6dd8c5e13d2fe.png)
Seria isso ?
Espero que esteja certo..
-
procyon
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Seg Out 31, 2011 23:40
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por MarceloFantini » Ter Nov 01, 2011 03:34
por MarceloFantini » Ter Nov 01, 2011 03:34
De fato, esqueci o

multiplicando. Desculpe.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Integral] Estou com dificuldade para resolver esta integral
por Paulo Perez » Qui Out 03, 2013 12:22
- 2 Respostas
- 4611 Exibições
- Última mensagem por Paulo Perez

Sex Out 04, 2013 16:32
Cálculo: Limites, Derivadas e Integrais
-
- [INTEGRAL] Integral por partes! Alguem pode me ajudar?
por mih123 » Qua Jan 16, 2013 20:18
- 3 Respostas
- 4579 Exibições
- Última mensagem por adauto martins

Qua Out 22, 2014 09:11
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Resolver Integral definida com trigonometria
por rodrigoboreli » Dom Set 07, 2014 01:02
- 1 Respostas
- 4342 Exibições
- Última mensagem por adauto martins

Sex Out 17, 2014 12:39
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Integral funçao trigonometrica
por ewald » Qua Ago 17, 2011 22:33
- 2 Respostas
- 2841 Exibições
- Última mensagem por ewald

Qui Ago 18, 2011 00:54
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Integral funçao trigonometrica
por ewald » Sáb Ago 20, 2011 17:20
- 2 Respostas
- 2865 Exibições
- Última mensagem por LuizAquino

Dom Ago 21, 2011 21:14
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
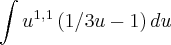
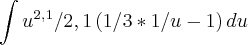 , estou fazendo errado?...por favor me expliquem!
, estou fazendo errado?...por favor me expliquem!
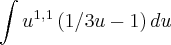
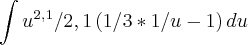 , estou fazendo errado?...por favor me expliquem!
, estou fazendo errado?...por favor me expliquem!
 . Para fazer um produto, use
. Para fazer um produto, use  .
.


 , (não sei se está certo).
, (não sei se está certo).
 . É isso? Ainda não entendo porque apareceria um expoente fracionário.
. É isso? Ainda não entendo porque apareceria um expoente fracionário.

![\int u^{1,1}. \left( \frac{1}{3u} -1 \right).du \\
\\
\text{Distribuindo os fatores:} \\
\\
\int \left[ u^{1,1}. \frac{1}{3u} -1 . u^{1,1} \right]du\\
\\
\text{Distribuindo as potencias:} \\
\\
\int \left[ \frac{u^{1}.u^{0,1}}{3u} -1 . u^{1,1} \right]du \\
\\
\text{Cortando o que puder e usando a propriedade da diferenca de uma integral:} \\
\\
\frac{1}{3} \int u^{0,1}.du - \int u^{1,1}du \\
\\
\text{Integrando temos:} \\
\\
\left[ \frac{1}{3} . \frac{u^{1,1}}{1,1} - \frac{u^{2,1}}{2,1} \right] + C \\
\\
\text{E finalmente:} \\
\\
\frac{u^{1,1}}{3,3} - \frac{u^{2,1}}{2,1} + C \int u^{1,1}. \left( \frac{1}{3u} -1 \right).du \\
\\
\text{Distribuindo os fatores:} \\
\\
\int \left[ u^{1,1}. \frac{1}{3u} -1 . u^{1,1} \right]du\\
\\
\text{Distribuindo as potencias:} \\
\\
\int \left[ \frac{u^{1}.u^{0,1}}{3u} -1 . u^{1,1} \right]du \\
\\
\text{Cortando o que puder e usando a propriedade da diferenca de uma integral:} \\
\\
\frac{1}{3} \int u^{0,1}.du - \int u^{1,1}du \\
\\
\text{Integrando temos:} \\
\\
\left[ \frac{1}{3} . \frac{u^{1,1}}{1,1} - \frac{u^{2,1}}{2,1} \right] + C \\
\\
\text{E finalmente:} \\
\\
\frac{u^{1,1}}{3,3} - \frac{u^{2,1}}{2,1} + C](/latexrender/pictures/40b37199df4fdb2befd6dd8c5e13d2fe.png)

