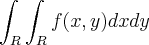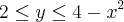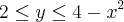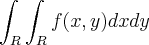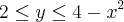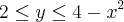por carvalhothg » Seg Out 17, 2011 20:51
Como calcular a integral abaixo?
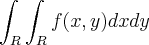
R é a região do primeiro quadrante limitado por:
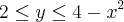
Minha duvida é como encontro os limites de integração em relação a x sendo que só foi dado:
-
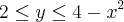
carvalhothg
- Usuário Dedicado
-
- Mensagens: 42
- Registrado em: Dom Set 04, 2011 18:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
por LuizAquino » Seg Out 17, 2011 22:10
Veja a ideia descrita no tópico abaixo e tente resolver esse exercício.
[Intregral]viewtopic.php?p=21751
-
LuizAquino
- Colaborador Moderador - Professor
-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Alguém pode me ajudar a resolver essa integral?
por V_Netto » Seg Jul 30, 2012 12:05
- 1 Respostas
- 1789 Exibições
- Última mensagem por Russman
Seg Jul 30, 2012 12:54
Cálculo: Limites, Derivadas e Integrais
-
- [INTEGRAL] Integral por partes! Alguem pode me ajudar?
por mih123 » Qua Jan 16, 2013 20:18
- 3 Respostas
- 4418 Exibições
- Última mensagem por adauto martins
Qua Out 22, 2014 09:11
Cálculo: Limites, Derivadas e Integrais
-
- Alguem pode ajudar-me?
por carlos r m oliveira » Seg Out 05, 2009 11:35
- 1 Respostas
- 2433 Exibições
- Última mensagem por Neperiano
Dom Jul 03, 2011 21:05
Estatística
-
- Alguém pode me ajudar?
por apoliveirarj » Seg Jul 19, 2010 18:20
- 1 Respostas
- 3286 Exibições
- Última mensagem por Douglasm
Seg Jul 19, 2010 18:49
Matemática Financeira
-
- Alguém pode me ajudar?
por Andromeda » Seg Set 19, 2011 20:19
- 2 Respostas
- 2274 Exibições
- Última mensagem por Andromeda
Seg Set 19, 2011 21:13
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Balanar - Seg Ago 09, 2010 04:01
Simplifique a expressão com radicais duplos abaixo:
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
Resposta:
Dica:
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
(dica : igualar a expressão a
e elevar ao quadrado os dois lados)
Assunto:
Simplifique a expressão com radicais duplos
Autor:
MarceloFantini - Qua Ago 11, 2010 05:46
É só fazer a dica.
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Soprano - Sex Mar 04, 2016 09:49
Olá,
O resultado é igual a 1, certo?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
