 por beel » Ter Out 04, 2011 22:30
por beel » Ter Out 04, 2011 22:30
Tendo a função
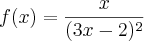
, a reta tangente ao gráfico de f no ponto (a,f(a)) é horizontal quando "a" vale quanto?
Eu pensei assim:
Y-Yo = Y'(Xo)(X - Xo)
Como a reta é horizontal, o coeficiente angular =derivada= Y'(Xo) é zero, assim
Y-f(a) = 0(X -Xo)
Y=f (a)
Y=
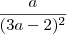
mas travei...
-
beel
- Colaborador Voluntário

-
- Mensagens: 172
- Registrado em: Sex Ago 26, 2011 13:14
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por LuizAquino » Qua Out 05, 2011 10:17
por LuizAquino » Qua Out 05, 2011 10:17
isanobile escreveu:(...)
Como a reta é horizontal, o coeficiente angular =derivada= Y'(Xo) é zero
(...)
Já que você sabe dessa informação, então por que você não simplesmente pensou em resolver a equação
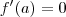
?
Note que faltou você pensar nisso para conseguir resolver o exercício!
Agora continue a resolução. Se a dúvida persistir, então poste aqui até onde você conseguiu desenvolver.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por beel » Sex Out 07, 2011 20:31
por beel » Sex Out 07, 2011 20:31
Entendi...fiquei em duvida se podia simplificar uma parte
(...)
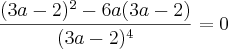
(...)
então fiz distributiva mesmo e meu resultado deu -2/3
-
beel
- Colaborador Voluntário

-
- Mensagens: 172
- Registrado em: Sex Ago 26, 2011 13:14
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por LuizAquino » Sáb Out 08, 2011 17:47
por LuizAquino » Sáb Out 08, 2011 17:47
isanobile escreveu: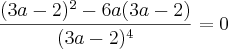
então fiz distributiva mesmo e meu resultado deu -2/3
O resultado é esse mesmo. Temos que
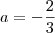
.
Quanto a simplificar essa expressão, se
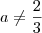
, então podemos escrever que:
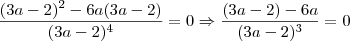
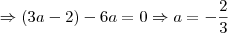
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por beel » Dom Out 09, 2011 13:57
por beel » Dom Out 09, 2011 13:57
Aaa sim, obrigada.
-
beel
- Colaborador Voluntário

-
- Mensagens: 172
- Registrado em: Sex Ago 26, 2011 13:14
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Calculo 1] reta tangente
por caiofisico » Ter Set 27, 2011 18:38
- 4 Respostas
- 1813 Exibições
- Última mensagem por caiofisico

Ter Set 27, 2011 22:02
Cálculo: Limites, Derivadas e Integrais
-
- Cálculo I: Reta Tangente e Área da função.
por Jhonata » Ter Fev 26, 2013 12:47
- 1 Respostas
- 1442 Exibições
- Última mensagem por young_jedi

Sex Mar 01, 2013 22:22
Cálculo: Limites, Derivadas e Integrais
-
- [DERIVADA] Reta tangente e Reta perpendicular
por antonelli2006 » Ter Nov 22, 2011 11:21
- 1 Respostas
- 8672 Exibições
- Última mensagem por LuizAquino

Ter Nov 22, 2011 14:28
Cálculo: Limites, Derivadas e Integrais
-
- [Reta Paralela à Reta Tangente]
por raimundoocjr » Qui Mai 30, 2013 18:44
- 0 Respostas
- 1156 Exibições
- Última mensagem por raimundoocjr

Qui Mai 30, 2013 18:44
Cálculo: Limites, Derivadas e Integrais
-
- Reta tangente
por AlbertoAM » Sáb Abr 30, 2011 15:32
- 1 Respostas
- 1530 Exibições
- Última mensagem por FilipeCaceres

Sáb Abr 30, 2011 19:13
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
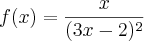 , a reta tangente ao gráfico de f no ponto (a,f(a)) é horizontal quando "a" vale quanto?
, a reta tangente ao gráfico de f no ponto (a,f(a)) é horizontal quando "a" vale quanto?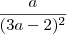


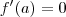 ?
?
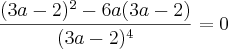
 .
.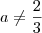 , então podemos escrever que:
, então podemos escrever que: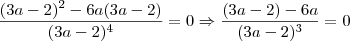
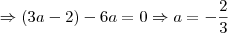
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
