Nunca tinha visto exemplos como elas. Quero aprender mais, porém queria ajuda para resolver essas duas questões.
1- Achar as dimensões do lote com menor área onde um edifício de 2000
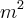de base possa ser construído, sendo exigido, recuo de 5 metros na frente e nos fundos e de 4 metros nas laterias. (Não consegui montar a formula e por causa desse recuo de 5 metro na frente e nos fundo e 4 metros nas laterais.) Como seria a montagem da formula?2-Qual deve ser a menor largura de um corredor para que vigas de aço de 12,5m de comprimento possam ter movimentação horizontal ao longo de uma certa passagem de 2,7m de largura e deve entrar num corredor que é perpendicular a passagem sem causar prejuízos a construção (despreze a espessura da viga).
.
: