Problema sobre limites incluindo geometria analítica

[Tiagovla]

Galera. Tentei o seguinte:
P = (x,x²).Então a interseção da mediana é o ponto .
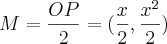Tendo a fórmula de ângulos de retas perpendiculares: m*m1=-1 e que a f'(x)=2x
Não sei se é valida a afirmativa:

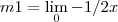
Pois com esta não consigo a resposta correta.
Assim: utilizei que o coeficiente angular é= -x/x² (conceito de tangente do triângulo retângulo). (Também não sei se pode ser provado assim).
Quando utilizo o ponto M. E o coeficiente angular: -x/x² em:
y-yo=m1(x-xo)
Para após calcular a interseção com a reta x=0. Ou seja, quando x tender a 0. Obtenho o resultado: -1/2.
Quando utilizo: y=m1x+Q
Obtenho 1/2 ( que é o correto).
Usando o conceito de Limites, como poderei responder a questão?
Invervalo: [0,1/2]
Espero uma ajuda : )

[LuizAquino]

Tiagovla, seja bem-vindo ao fórum.

Como essa foi sua primeira mensagem, vale destacar alguns pontos:

1. Não envie o texto do exercício como uma imagem. Isso prejudica os sistemas de busca. Envie como imagem apenas o que for necessário, digitando todo o resto;
2. Você tem disponível na edição de suas mensagens a opção TeX, que serve para digitar todas as notações matemáticas de forma mais conveniente. Se precisar, use também o Editor de Fórmulas.

Dito isso, vejamos o exercício. A animação abaixo ilustra a situação.

parábola.gif (83.13 KiB) Exibido 1377 vezes

Como P é um ponto da parábola y = x², então ele tem o formato (k, k²), para algum k real.

A reta que passa por O = (0, 0) e P tem equação y = kx.

O ponto médio M do segmento OP será dado por .

Sabemos que a reta que passa por Q e M é perpendicular a reta y = kx. Isso significa que o coeficiente angular dessa reta é -1/k. Considerando que conhecemos o ponto M, podemos determinar que a equação dessa reta é dada por . Como a interseção dessa reta com o eixo y é o ponto Q, podemos dizer que esse ponto é dado por .

Note que para fazer P tender ao vértice da parábola basta fazer k tender a 0.

Agora tente terminar o exercício.