Bem, é mais comum analisar assíntotas verticais em funções racionais do tipo:

, onde P(x) e Q(x) são polinômios. Nesse caso, em particular, é comum e muito prático analisar o domínio da função, e se existe algum ponto x onde a função não está definida no domínio, então esse ponto supostamente será uma assíntota vertical. É sempre indispensável e necessário fazer a verificação dessa observação pelos limites laterais no(s) ponto(s) em que f não está definida, e se f(x) tende a menos ou mais infinito, conclui-se que, de fato, aquele ponto é uma assíntota vertical.
OBS: Há casos que é possível simplificar a função e observar o domínio pode nem ser sempre útil ou até desnecessário.
Por exemplo, temos a função
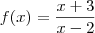
.
Podemos observar que no ponto x = 2, f(x) não está definido e se usarmos a ideia intuitiva de limites, tomando valores arbitrários para x bem próximos de 2, mas diferente de 2. Isto é, x tende a 2, mas é diferente de 2 por ambos os lados, vemos que f(x) tente a +infinito pela direita e -infinito pela esquerda.
Experimente fazendo, por exemplo, x = 1.9999 (um valor de x pela esquerda) e x = 2.0001 (um valor de x pela direita)... Encontrará números muito grandes, negativos pela esquerda e positivos pela direita. (:
Espero que essa informação ajude de algum modo.
Abraço.
O_O Alguns minutos depois, vi que o tópico é velho... Bem, de qualquer modo, não apagarei meu post... De repente ajuda alguém. D:
K




 , onde P(x) e Q(x) são polinômios. Nesse caso, em particular, é comum e muito prático analisar o domínio da função, e se existe algum ponto x onde a função não está definida no domínio, então esse ponto supostamente será uma assíntota vertical. É sempre indispensável e necessário fazer a verificação dessa observação pelos limites laterais no(s) ponto(s) em que f não está definida, e se f(x) tende a menos ou mais infinito, conclui-se que, de fato, aquele ponto é uma assíntota vertical.
, onde P(x) e Q(x) são polinômios. Nesse caso, em particular, é comum e muito prático analisar o domínio da função, e se existe algum ponto x onde a função não está definida no domínio, então esse ponto supostamente será uma assíntota vertical. É sempre indispensável e necessário fazer a verificação dessa observação pelos limites laterais no(s) ponto(s) em que f não está definida, e se f(x) tende a menos ou mais infinito, conclui-se que, de fato, aquele ponto é uma assíntota vertical.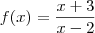 .
.
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)