![\lim_{x\rightarrow\infty}\left(\sqrt[2]{9x^2+x }-3x \right) \lim_{x\rightarrow\infty}\left(\sqrt[2]{9x^2+x }-3x \right)](/latexrender/pictures/2325e98bef91714b9c772acb2e8b39d7.png)
a resolução fica assim:
![\lim_{x\rightarrow\infty}\left(\sqrt[2]{9x^2+x }-3x \right). \frac{\left(\sqrt[2]{9x^2+x }+3x \right)}{\left(\sqrt[2]{9x^2+x }+3x \right)}= \frac{1}{6} \lim_{x\rightarrow\infty}\left(\sqrt[2]{9x^2+x }-3x \right). \frac{\left(\sqrt[2]{9x^2+x }+3x \right)}{\left(\sqrt[2]{9x^2+x }+3x \right)}= \frac{1}{6}](/latexrender/pictures/9dd8ccf67ab708c77b4d2a1e6b2f01d3.png)
Porquê eu preciso fazer esse trabalho de multiplicar toda expressão por
![{\left(\sqrt[2]{9x^2+x }+3x \right)} {\left(\sqrt[2]{9x^2+x }+3x \right)}](/latexrender/pictures/9f11e9bed96a34d1fafb572250ac0949.png)
digo isso porque após esse passo, eu terei de dividir o numerador e denominador por x correto? Se eu,antes de multiplicar a minha equaçao por esse termo ja dividisse tudo por x ficaria assim:
![\frac{{\left(\sqrt[2]{9x^2+x }-3x \right)}}{x}= \frac{\sqrt[2]{9x^2+x}}{x}-\frac{3x}{x}= \sqrt[2]{\frac{9x^2+x}{x^2}}-3= 3-3=0 \frac{{\left(\sqrt[2]{9x^2+x }-3x \right)}}{x}= \frac{\sqrt[2]{9x^2+x}}{x}-\frac{3x}{x}= \sqrt[2]{\frac{9x^2+x}{x^2}}-3= 3-3=0](/latexrender/pictures/3be728c25c18f41af6183156bd5b7be2.png)
A resposta é errada. Todavia, não consigo enxergar no caminho a impossibilidade de fazer esse cálculo dessa maneira.
Por fim, oque então me faz pensar que é necessário fazer:
![\lim_{x\rightarrow\infty}\left(\sqrt[2]{9x^2+x }-3x \right). \frac{\left(\sqrt[2]{9x^2+x }+3x \right)}{\left(\sqrt[2]{9x^2+x }+3x \right)}= \frac{1}{6} \lim_{x\rightarrow\infty}\left(\sqrt[2]{9x^2+x }-3x \right). \frac{\left(\sqrt[2]{9x^2+x }+3x \right)}{\left(\sqrt[2]{9x^2+x }+3x \right)}= \frac{1}{6}](/latexrender/pictures/9dd8ccf67ab708c77b4d2a1e6b2f01d3.png)


 . Você multiplicou e dividiu tudo por isso.
. Você multiplicou e dividiu tudo por isso. , pois desse modo podemos usar o fato de que se
, pois desse modo podemos usar o fato de que se 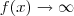 , então
, então 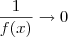 .
. (com x não nulo e diferente de 1). Por outro lado, temos que
(com x não nulo e diferente de 1). Por outro lado, temos que  (com x não nulo).
(com x não nulo). .
.
