 por killerkill » Dom Ago 21, 2011 14:13
por killerkill » Dom Ago 21, 2011 14:13
Estava fazendo exercícios aqui me veio uma dúvida. Antes vou mostrar a questão aqui pra poder me explicar melhor.
![\lim_{x\rightarrow\infty}\left(\sqrt[2]{9x^2+x }-3x \right) \lim_{x\rightarrow\infty}\left(\sqrt[2]{9x^2+x }-3x \right)](/latexrender/pictures/2325e98bef91714b9c772acb2e8b39d7.png)
a resolução fica assim:
![\lim_{x\rightarrow\infty}\left(\sqrt[2]{9x^2+x }-3x \right). \frac{\left(\sqrt[2]{9x^2+x }+3x \right)}{\left(\sqrt[2]{9x^2+x }+3x \right)}= \frac{1}{6} \lim_{x\rightarrow\infty}\left(\sqrt[2]{9x^2+x }-3x \right). \frac{\left(\sqrt[2]{9x^2+x }+3x \right)}{\left(\sqrt[2]{9x^2+x }+3x \right)}= \frac{1}{6}](/latexrender/pictures/9dd8ccf67ab708c77b4d2a1e6b2f01d3.png)
Porquê eu preciso fazer esse trabalho de multiplicar toda expressão por
![{\left(\sqrt[2]{9x^2+x }+3x \right)} {\left(\sqrt[2]{9x^2+x }+3x \right)}](/latexrender/pictures/9f11e9bed96a34d1fafb572250ac0949.png)
digo isso porque após esse passo, eu terei de dividir o numerador e denominador por x correto? Se eu,antes de multiplicar a minha equaçao por esse termo ja dividisse tudo por x ficaria assim:
![\frac{{\left(\sqrt[2]{9x^2+x }-3x \right)}}{x}= \frac{\sqrt[2]{9x^2+x}}{x}-\frac{3x}{x}= \sqrt[2]{\frac{9x^2+x}{x^2}}-3= 3-3=0 \frac{{\left(\sqrt[2]{9x^2+x }-3x \right)}}{x}= \frac{\sqrt[2]{9x^2+x}}{x}-\frac{3x}{x}= \sqrt[2]{\frac{9x^2+x}{x^2}}-3= 3-3=0](/latexrender/pictures/3be728c25c18f41af6183156bd5b7be2.png)
A resposta é errada. Todavia, não consigo enxergar no caminho a impossibilidade de fazer esse cálculo dessa maneira.
Por fim, oque então me faz pensar que é necessário fazer:
![\lim_{x\rightarrow\infty}\left(\sqrt[2]{9x^2+x }-3x \right). \frac{\left(\sqrt[2]{9x^2+x }+3x \right)}{\left(\sqrt[2]{9x^2+x }+3x \right)}= \frac{1}{6} \lim_{x\rightarrow\infty}\left(\sqrt[2]{9x^2+x }-3x \right). \frac{\left(\sqrt[2]{9x^2+x }+3x \right)}{\left(\sqrt[2]{9x^2+x }+3x \right)}= \frac{1}{6}](/latexrender/pictures/9dd8ccf67ab708c77b4d2a1e6b2f01d3.png)
-
killerkill
- Usuário Dedicado

-
- Mensagens: 25
- Registrado em: Ter Ago 09, 2011 22:39
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eg. Elétrica
- Andamento: cursando
 por LuizAquino » Dom Ago 21, 2011 20:59
por LuizAquino » Dom Ago 21, 2011 20:59
killerkill escreveu:![\lim_{x\rightarrow\infty}\left(\sqrt[2]{9x^2+x }-3x \right) \lim_{x\rightarrow\infty}\left(\sqrt[2]{9x^2+x }-3x \right)](/latexrender/pictures/2325e98bef91714b9c772acb2e8b39d7.png)
a resolução fica assim:
![\lim_{x\rightarrow\infty}\left(\sqrt[2]{9x^2+x }-3x \right). \frac{\left(\sqrt[2]{9x^2+x }+3x \right)}{\left(\sqrt[2]{9x^2+x }+3x \right)}= \frac{1}{6} \lim_{x\rightarrow\infty}\left(\sqrt[2]{9x^2+x }-3x \right). \frac{\left(\sqrt[2]{9x^2+x }+3x \right)}{\left(\sqrt[2]{9x^2+x }+3x \right)}= \frac{1}{6}](/latexrender/pictures/9dd8ccf67ab708c77b4d2a1e6b2f01d3.png)
Porquê eu preciso fazer esse trabalho de multiplicar toda expressão por
![{\left(\sqrt[2]{9x^2+x }+3x \right)} {\left(\sqrt[2]{9x^2+x }+3x \right)}](/latexrender/pictures/9f11e9bed96a34d1fafb572250ac0949.png)
Em primeiro lugar, você não
apenas multiplicou tudo por

. Você multiplicou e dividiu tudo por isso.
Em segundo lugar, a ideia básica é reescrever o limite de modo a aparecer termos como

, pois desse modo podemos usar o fato de que se
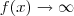
, então
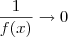
.
killerkill escreveu:Se eu,antes de multiplicar a minha equaçao por esse termo ja dividisse tudo por x ficaria assim:
![\frac{{\left(\sqrt[2]{9x^2+x }-3x \right)}}{x}= \frac{\sqrt[2]{9x^2+x}}{x}-\frac{3x}{x}= \sqrt[2]{\frac{9x^2+x}{x^2}}-3= 3-3=0 \frac{{\left(\sqrt[2]{9x^2+x }-3x \right)}}{x}= \frac{\sqrt[2]{9x^2+x}}{x}-\frac{3x}{x}= \sqrt[2]{\frac{9x^2+x}{x^2}}-3= 3-3=0](/latexrender/pictures/3be728c25c18f41af6183156bd5b7be2.png)
A resposta é errada.
É claro que está errado! Por exemplo, veja que

(com x não nulo e diferente de 1). Por outro lado, temos que

(com x não nulo).
Isso significa que para não alterar a expressão você deveria multiplicar e dividir tudo por x. Entretanto, mesmo que nesse exercício você fizesse isso, veria que não ajudaria na solução, pois acabaria em uma indeterminação do tipo

.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [limites no infinito]Limite no infinito de um ponto finito
por moyses » Ter Ago 30, 2011 12:45
- 3 Respostas
- 3528 Exibições
- Última mensagem por LuizAquino

Ter Ago 30, 2011 18:57
Cálculo: Limites, Derivadas e Integrais
-
- [limites] limite no infinito
por baloso » Qua Abr 30, 2014 17:19
- 3 Respostas
- 2106 Exibições
- Última mensagem por Russman

Qui Mai 01, 2014 15:26
Cálculo: Limites, Derivadas e Integrais
-
- [LIMITE] limites no infinito com raízes
por camila_braz » Dom Jun 11, 2017 11:42
- 0 Respostas
- 3045 Exibições
- Última mensagem por camila_braz

Dom Jun 11, 2017 11:42
Cálculo: Limites, Derivadas e Integrais
-
- [LIMITE] Limites que tendem ao infinito com raízes
por Mell » Qua Mai 01, 2013 15:21
- 3 Respostas
- 2866 Exibições
- Última mensagem por e8group

Sáb Mai 04, 2013 02:41
Cálculo: Limites, Derivadas e Integrais
-
- [Limites] Ajuda com limites no infinito e continuidade
 por umbrorz » Dom Abr 15, 2012 00:54
por umbrorz » Dom Abr 15, 2012 00:54
- 3 Respostas
- 4779 Exibições
- Última mensagem por umbrorz

Seg Abr 16, 2012 11:46
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\lim_{x\rightarrow\infty}\left(\sqrt[2]{9x^2+x }-3x \right) \lim_{x\rightarrow\infty}\left(\sqrt[2]{9x^2+x }-3x \right)](/latexrender/pictures/2325e98bef91714b9c772acb2e8b39d7.png)
![\lim_{x\rightarrow\infty}\left(\sqrt[2]{9x^2+x }-3x \right). \frac{\left(\sqrt[2]{9x^2+x }+3x \right)}{\left(\sqrt[2]{9x^2+x }+3x \right)}= \frac{1}{6} \lim_{x\rightarrow\infty}\left(\sqrt[2]{9x^2+x }-3x \right). \frac{\left(\sqrt[2]{9x^2+x }+3x \right)}{\left(\sqrt[2]{9x^2+x }+3x \right)}= \frac{1}{6}](/latexrender/pictures/9dd8ccf67ab708c77b4d2a1e6b2f01d3.png)
![{\left(\sqrt[2]{9x^2+x }+3x \right)} {\left(\sqrt[2]{9x^2+x }+3x \right)}](/latexrender/pictures/9f11e9bed96a34d1fafb572250ac0949.png)
![\frac{{\left(\sqrt[2]{9x^2+x }-3x \right)}}{x}= \frac{\sqrt[2]{9x^2+x}}{x}-\frac{3x}{x}= \sqrt[2]{\frac{9x^2+x}{x^2}}-3= 3-3=0 \frac{{\left(\sqrt[2]{9x^2+x }-3x \right)}}{x}= \frac{\sqrt[2]{9x^2+x}}{x}-\frac{3x}{x}= \sqrt[2]{\frac{9x^2+x}{x^2}}-3= 3-3=0](/latexrender/pictures/3be728c25c18f41af6183156bd5b7be2.png)
![\lim_{x\rightarrow\infty}\left(\sqrt[2]{9x^2+x }-3x \right). \frac{\left(\sqrt[2]{9x^2+x }+3x \right)}{\left(\sqrt[2]{9x^2+x }+3x \right)}= \frac{1}{6} \lim_{x\rightarrow\infty}\left(\sqrt[2]{9x^2+x }-3x \right). \frac{\left(\sqrt[2]{9x^2+x }+3x \right)}{\left(\sqrt[2]{9x^2+x }+3x \right)}= \frac{1}{6}](/latexrender/pictures/9dd8ccf67ab708c77b4d2a1e6b2f01d3.png)


 . Você multiplicou e dividiu tudo por isso.
. Você multiplicou e dividiu tudo por isso. , pois desse modo podemos usar o fato de que se
, pois desse modo podemos usar o fato de que se 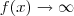 , então
, então 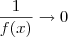 .
. (com x não nulo e diferente de 1). Por outro lado, temos que
(com x não nulo e diferente de 1). Por outro lado, temos que  (com x não nulo).
(com x não nulo). .
.