 por futuro fisico » Sáb Jun 25, 2011 18:55
por futuro fisico » Sáb Jun 25, 2011 18:55
minha duvida é a seguinte
como resolver esta integral

.
tentei integração por partes e me deparei com mais 3 integrais e depois com mais duas.
Não precisa a resolução toda, so preciso da ideia, o resto desenvolvo.
desde ja agradeço!
P.S.: sou novo, favor desconsiderar erro no post.
-
futuro fisico
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Sáb Jun 25, 2011 18:40
- Formação Escolar: GRADUAÇÃO
- Área/Curso: fisica medica
- Andamento: cursando
 por nietzsche » Sáb Jun 25, 2011 22:06
por nietzsche » Sáb Jun 25, 2011 22:06
olá futuro físico,
usando a identidade
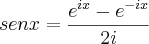
você simplifica essa integral. aí dá pra resolver usando integração por partes mais facilmente.
abraço
-
nietzsche
- Usuário Parceiro

-
- Mensagens: 99
- Registrado em: Qua Jan 12, 2011 14:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por LuizAquino » Sáb Jun 25, 2011 22:31
por LuizAquino » Sáb Jun 25, 2011 22:31
DicaUse a identidade:
![\textrm{sen}\,x\, \textrm{sen}\,y = \frac {1}{2}[{\cos(x-y) - \cos(x+y)] \textrm{sen}\,x\, \textrm{sen}\,y = \frac {1}{2}[{\cos(x-y) - \cos(x+y)]](/latexrender/pictures/5a93d572270e969bb9ade2726066b072.png)
.
A integral original será transformada em duas. Para resolver cada uma dessas integrais será necessário utilizar duas vezes a integração por partes.
Vale ainda lembrar que:
(i)

, com
k uma constante não nula.
(ii)
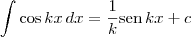
, com
k uma constante não nula.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por MarceloFantini » Dom Jun 26, 2011 01:29
por MarceloFantini » Dom Jun 26, 2011 01:29
Nietzsche, acredito que não seja necessário ferramental de complexos nesta questão.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por nietzsche » Dom Jun 26, 2011 18:38
por nietzsche » Dom Jun 26, 2011 18:38
eu dei apenas uma dica. geralmente os problemas de matemática tem mais de um jeito de fazer.
-
nietzsche
- Usuário Parceiro

-
- Mensagens: 99
- Registrado em: Qua Jan 12, 2011 14:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por MarceloFantini » Dom Jun 26, 2011 18:41
por MarceloFantini » Dom Jun 26, 2011 18:41
Tem, mas concorda que é um tremendo canhão pra resolver uma questão simples? Haha. Além do mais, depende de ele saber o que
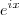
significa, o que não necessariamente simplifica as coisas.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por nietzsche » Dom Jun 26, 2011 20:27
por nietzsche » Dom Jun 26, 2011 20:27
não acho tremendo canhão. seria um tremendo canhão se ele fosse resolver por séries de fourier. se ele está tentando resolver uma integral desse tipo, ele já deve conhecer as propriedades básicas dos números complexos. eu acho mais fácil decorar a fórmula de euler do que as fórmulas de produto, soma, etc, de funções trigonométricas. cada um tem suas preferências.
e se vc tem uma forma mais fácil de resolver o problema, faça que nem luiz aquino, exponha e deixe que o dono da dúvida escolha. criticar é muito fácil.
-
nietzsche
- Usuário Parceiro

-
- Mensagens: 99
- Registrado em: Qua Jan 12, 2011 14:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por MarceloFantini » Dom Jun 26, 2011 20:36
por MarceloFantini » Dom Jun 26, 2011 20:36
Nietzsche, quero começar o post esclarecendo que não tenho a intenção de criticá-lo de forma alguma, estamos apenas conversando e quero deixar claro que se em algum momento fiz comentários que soassem ofensivos peço desculpas. Eu concordo com você que se está estudando integrais provavelmente ele viu propriedades básicas de números complexos, mas visto o ensino médio que tive (e que muitas pessoas que converso tiveram, e mesmo uma grande maioria dos usuários daqui tiveram), a identidade de Euler não foi vista durante esse período, e decorar sem entender é um tanto quanto ruim sem entender direito o porque. Também concordo que a vantagem dela é que é muito mais fácil memorizar do que produtos e somas de funções trigonométricas, então ponto positivo. Por último, não encontrei maneira mais fácil de resolver o problema que a do Luiz Aquino, portanto não tive nada a acrescentar quanto a resolução da questão.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por LuizAquino » Dom Jun 26, 2011 23:17
por LuizAquino » Dom Jun 26, 2011 23:17
Prezados,
Apenas para completar a conversa, na primeira disciplina de Cálculo tipicamente apenas são abordas funções de uma variável real. Ou seja, é estudado como calcular limites, derivadas e integrais envolvendo essas funções. Por essa razão, não é apropriado usar identidades complexas nesse momento. Por outro lado, se já houve o estudo de integrais de funções complexas, aí sim o uso dessas identidades seria natural.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por nietzsche » Ter Jun 28, 2011 00:03
por nietzsche » Ter Jun 28, 2011 00:03
concordo com vc luiz aquino. mas como não se sabe se o dono da dúvida está num primeiro curso, vale postar todas formas possíveis.
se ele for físico, pra ele essa integral pode ter propriedades de alguma teoria da física que aparecerão manipulando as diferentes formas de resolvê-la.
-
nietzsche
- Usuário Parceiro

-
- Mensagens: 99
- Registrado em: Qua Jan 12, 2011 14:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por LuizAquino » Ter Jun 28, 2011 09:29
por LuizAquino » Ter Jun 28, 2011 09:29
nietzsche escreveu:concordo com vc Luiz Aquino. mas como não se sabe se o dono da dúvida está num primeiro curso, vale postar todas formas possíveis.
Bem, o meu palpite é que ele está estudando apenas integrais com funções de uma variável real.
E então
futuro fisico, em que curso de Cálculo você está? Nesse curso foi estudado integrais de funções complexas?
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por nietzsche » Ter Jun 28, 2011 10:31
por nietzsche » Ter Jun 28, 2011 10:31
fazendo oq eu disse ele vai perceber que não precisamos integrar uma função complexa. manipulando a fórmula de euler, ele tranforma senos em cossenos com argumentos reais. aí é só integrar uma soma, ou produto de dois termos.
pra passar no vestibular eu tive que saber usar a fórmula de euler. creio que ele tenha ouvido falar que existe uma certa fórmula de euler.
-
nietzsche
- Usuário Parceiro

-
- Mensagens: 99
- Registrado em: Qua Jan 12, 2011 14:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por futuro fisico » Sáb Jul 02, 2011 17:08
por futuro fisico » Sáb Jul 02, 2011 17:08
consegui responder valeu
na verdade essa era uma questao de MFT I(Metodos de Fisica Teorica I), para desenvolver a série de fourier.
obrigado a todos
-
futuro fisico
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Sáb Jun 25, 2011 18:40
- Formação Escolar: GRADUAÇÃO
- Área/Curso: fisica medica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- 2º TFC para integrais. Ajuda
por dagoth » Qui Dez 16, 2010 21:34
- 1 Respostas
- 1683 Exibições
- Última mensagem por Neperiano

Seg Dez 20, 2010 22:27
Cálculo: Limites, Derivadas e Integrais
-
- [Integrais] Preciso de ajuda com esse cálculo...
por phvicari » Sáb Set 03, 2011 04:40
- 3 Respostas
- 1872 Exibições
- Última mensagem por LuizAquino

Dom Set 04, 2011 13:30
Cálculo: Limites, Derivadas e Integrais
-
- [Derivadas/Integrais] Ajuda com 5 questões de cálculo
por matheuskns » Sex Nov 28, 2014 20:27
- 1 Respostas
- 1873 Exibições
- Última mensagem por Cleyson007

Sáb Nov 29, 2014 20:40
Cálculo: Limites, Derivadas e Integrais
-
- [integrais] Calculando áreas - Integrais
 por Faby » Seg Set 19, 2011 10:55
por Faby » Seg Set 19, 2011 10:55
- 11 Respostas
- 8837 Exibições
- Última mensagem por LuizAquino

Qua Set 21, 2011 18:03
Cálculo: Limites, Derivadas e Integrais
-
- Integrais
por pseytow » Qui Nov 27, 2008 21:54
- 1 Respostas
- 2811 Exibições
- Última mensagem por Adriano Tavares

Qui Mar 10, 2011 01:52
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 .
.

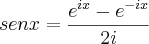 você simplifica essa integral. aí dá pra resolver usando integração por partes mais facilmente.
você simplifica essa integral. aí dá pra resolver usando integração por partes mais facilmente.
![\textrm{sen}\,x\, \textrm{sen}\,y = \frac {1}{2}[{\cos(x-y) - \cos(x+y)] \textrm{sen}\,x\, \textrm{sen}\,y = \frac {1}{2}[{\cos(x-y) - \cos(x+y)]](/latexrender/pictures/5a93d572270e969bb9ade2726066b072.png) .
. , com
, com 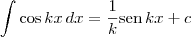 , com
, com 

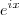 significa, o que não necessariamente simplifica as coisas.
significa, o que não necessariamente simplifica as coisas.
 .
.



