 por Deivid » Seg Jun 20, 2011 18:41
por Deivid » Seg Jun 20, 2011 18:41
Olá, eu estou com bastante dificuldades para resolver algumas questões de uma lista de exercícios que tenho aqui baseada no livro Cálculo B de Mirian Buss e Diva Flemming.
A questão é sobre máximos e mínimos e eu não sei nem como começar.
"Calcular as dimensões de uma caixa com base retangular, sem tampa, de volume máximo, com área lateral total igual a 5 cm²."
"Precisa-se construir um tanque com a forma de um paralelepípedo para estocar 270m³ de combustível, gastando a menor quantidade de material em sua construção. Supondo que todas as paredes são feitas do mesmo material e terão a mesma espessura, determinar as dimensões do tanque."
São as questões no estilo dessas duas que eu não consigo compreender. Alguém poderia dar uma luz?
Obrigado,
Deivid Steffens.
-
Deivid
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Ter Set 21, 2010 17:52
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
 por LuizAquino » Seg Jun 20, 2011 19:54
por LuizAquino » Seg Jun 20, 2011 19:54
Para determinar o máximo ou o mínimo local de uma função de duas variáveis podemos usar o teste da segunda derivada.
Seja

. Suponha que
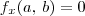
e

(com
f possuindo derivadas parciais contínuas até pelo menos a segunda ordem).
(i) Se
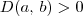
e

, então

é um mínimo local.
(ii) Se
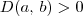
e

, então

é um máximo local.
(iii) Se
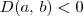
, então

não é nem mínimo e nem máximo local.
Desse modo, nesse tipo de exercício a primeira coisa que você precisa fazer é armar a função que deseja calcular o mínimo ou o máximo.
No caso particular dos exercícios que você enviou, note que essa parte de armar a função exige apenas os conhecimentos de Geometria Espacial. Portanto, é recomendável que você estude essa matéria caso não esteja sabendo.
SugestãoSe quiser revisar os conceitos de máximo ou mínimo de funções com uma variável, eu recomendo que assista as
vídeo-aulas:
- 19. Cálculo I - Máximo e Mínimo de Funções.
- 20. Cálculo I - Crescimento, Decrescimento e Concavidade do Gráfico de Funções.
- 21. Cálculo I - Teste da Primeira e da Segunda Derivada.
Editado pela última vez por
LuizAquino em Ter Jun 21, 2011 10:14, em um total de 4 vezes.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Deivid » Ter Jun 21, 2011 00:52
por Deivid » Ter Jun 21, 2011 00:52
Olá, obrigado pela resposta.
Seus vídeos me esclareceram algumas duvidas. Só para informar, eu tenho que resolver o exercício usando derivadas de mais variáveis, não uma.
Então analisando o primeiro problema eu tenho a informação que é uma caixa retangular, portanto volume é
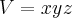
. E pela área informada eu obtenho
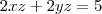
. A área total é

, portanto

.
Essas as informações que consegui coletar, estão corretas, como procedo agora?
Desculpe não conseguir avançar mais que isso, mas essa matéria realmente não entrou na minha cabeça.
-
Deivid
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Ter Set 21, 2010 17:52
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
 por LuizAquino » Ter Jun 21, 2011 10:08
por LuizAquino » Ter Jun 21, 2011 10:08
Deivid escreveu:Então analisando o primeiro problema eu tenho a informação que é uma caixa retangular, portanto volume é V=xyz. E pela área informada eu obtenho 2xz + 2yz=5. A área total é At=Al + Ab, portanto At = 2xz + 2yz + xy.
O exercício informa que a
área lateral total é igual a 5 cm². Portanto, temos que 2xz + 2yz + xy = 5.
Queremos maximizar o volume, que é dado por V = xyz. Ora, essa é uma função de três variáveis, mas queremos utilizar os conhecimentos sobre o máximo de funções com duas variáveis.
Para reduzir o número de variáveis dessa função, basta perceber que da informação sobre a área lateral total temos que z = (5 - xy)/(2x + 2y). Portanto, V pode ser reescrito como uma função de duas variáveis:

.
Agora basta utilizar o teste da segunda derivada.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Deivid » Qua Jun 22, 2011 17:06
por Deivid » Qua Jun 22, 2011 17:06
Infelizmente a primeira eu simplesmente não consegui fazer...
Mas a segunda eu consegui(tanque de 270m³), encontrei valores
![\left(3\sqrt[3]{10}, 3\sqrt[3]{10}, 3\sqrt[3]{10} \right) \left(3\sqrt[3]{10}, 3\sqrt[3]{10}, 3\sqrt[3]{10} \right)](/latexrender/pictures/f259531d86b480ab684525ac91dad146.png)
que coincidem com o da lista.
-
Deivid
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Ter Set 21, 2010 17:52
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
 por LuizAquino » Qua Jun 22, 2011 17:33
por LuizAquino » Qua Jun 22, 2011 17:33
Deivid escreveu:Infelizmente a primeira eu simplesmente não consegui fazer...
Que parte exatamente você não conseguiu fazer? Qual é exatamente a sua dúvida?
Você conseguiu calcular as derivadas parciais

e

?
Você conseguiu resolver o sistema abaixo?
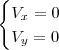
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por miguelfl » Qua Jun 22, 2011 21:21
por miguelfl » Qua Jun 22, 2011 21:21
é bom usar mutiplicadores de Lagrange, agora eu me confundi nessa parte das áreas laterias iguais a 5 porque aqui n dá quando eu coloco 2xy + 2 xz = 5
-
miguelfl
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Qua Jun 22, 2011 21:17
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Ambiental
- Andamento: cursando
 por Deivid » Qua Jun 22, 2011 23:15
por Deivid » Qua Jun 22, 2011 23:15
Não sei o que são multiplicadores de lagrange, vou dar uma pesquisada. Na verdade a area das laterais é 2xz(a parte frontal e traseira) + 2 yz(as duas laterias) = 5.
Luiz Aquino, não havia percebido que você editou sua primeira mensagem, eu já conhecia esses conceitos do determinante e dos testes, não sabia apenas quando aplica-los.
Uma duvida, quando o determinante der maior que 0 e a derivada der = 0, existe essa possibilidade? (se não existe errei uma questão na prova hoje hehe)
-
Deivid
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Ter Set 21, 2010 17:52
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
 por MarceloFantini » Qua Jun 22, 2011 23:44
por MarceloFantini » Qua Jun 22, 2011 23:44
Acredito que essa possibilidade não existe, pois segunda derivada igual a zero não se conclui nada.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por LuizAquino » Qua Jun 22, 2011 23:47
por LuizAquino » Qua Jun 22, 2011 23:47
miguelfl escreveu:(...) é bom usar mutiplicadores de Lagrange (...)
Acontece que os Multiplicadores de Lagrange tipicamente são abordados depois do conteúdo de máximo e mínimo de funções com várias variáveis. Por isso mesmo que eu não sugeri, pois pela primeira pergunta do Deivid percebe-se que ele ainda não estudou esse conteúdo, como de fato ele acabou confirmando.
miguelfl escreveu:agora eu me confundi nessa parte das áreas laterias iguais a 5 porque aqui n dá quando eu coloco 2xy + 2 xz = 5
Deivid escreveu:Na verdade a area das laterais é 2xz(a parte frontal e traseira) + 2 yz(as duas laterias) = 5.
O exercício diz que a área lateral
total é 5 cm². É para contabilizar a parte frontal, traseira, laterais e o fundo. Só não é para contabilizar a tampa, como sugere o texto do exercício. Por isso que ficamos com 2xz + 2yz + xy = 5.
Em verdade, o texto do exercício deveria estar mais claro. Por exemplo, poderia estar escrito que a superfície (ou a área) total da caixa é 5 cm².
ObservaçãoNa minha primeira mensagem, onde há escrito
Seja

.
leia-se
Seja

.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [maximos e minimos] Problemas de minimos e maximos
por amigao » Seg Jun 24, 2013 22:28
- 1 Respostas
- 3805 Exibições
- Última mensagem por young_jedi

Ter Jun 25, 2013 17:49
Cálculo: Limites, Derivadas e Integrais
-
- Maximos e minimos
por Maykids » Qui Jun 02, 2011 01:30
- 1 Respostas
- 1497 Exibições
- Última mensagem por LuizAquino

Qui Jun 02, 2011 15:17
Cálculo: Limites, Derivadas e Integrais
-
- Problema, mínimos e máximos
por Bruhh » Sex Jun 11, 2010 16:45
- 3 Respostas
- 2688 Exibições
- Última mensagem por Bruhh

Sex Jun 11, 2010 16:53
Cálculo: Limites, Derivadas e Integrais
-
- Minimos e Maximos locais
por aline_n » Seg Jun 06, 2011 22:36
- 1 Respostas
- 1342 Exibições
- Última mensagem por LuizAquino

Ter Jun 07, 2011 11:32
Cálculo: Limites, Derivadas e Integrais
-
- Otimização (Maximos e Minimos)
por Maykids » Sex Jun 24, 2011 03:49
- 4 Respostas
- 3990 Exibições
- Última mensagem por LuizAquino

Sáb Jun 25, 2011 16:58
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 . Suponha que
. Suponha que 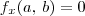 e
e  (com
(com 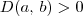 e
e  , então
, então  é um mínimo local.
é um mínimo local. , então
, então 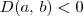 , então
, então 
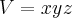 . E pela área informada eu obtenho
. E pela área informada eu obtenho 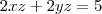 . A área total é
. A área total é  , portanto
, portanto  .
. .
.![\left(3\sqrt[3]{10}, 3\sqrt[3]{10}, 3\sqrt[3]{10} \right) \left(3\sqrt[3]{10}, 3\sqrt[3]{10}, 3\sqrt[3]{10} \right)](/latexrender/pictures/f259531d86b480ab684525ac91dad146.png) que coincidem com o da lista.
que coincidem com o da lista. e
e  ?
?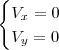


 .
.

 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.