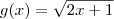 em p = 1
em p = 1Eu desenvolvi e cheguei até isso:
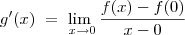 = ... =
= ... = 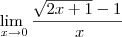
Eu imagino que eu preciso cancelar alguma coisa nesse limite para não dar indefinição, mas eu não consigo pensar em nenhuma forma de fazer isso.

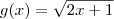 em p = 1
em p = 1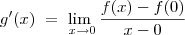 = ... =
= ... = 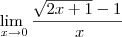

![\frac{\sqrt[]{2x+1}}{x}-\frac{1}{x} \frac{\sqrt[]{2x+1}}{x}-\frac{1}{x}](/latexrender/pictures/847eea802f855cd412ebc8940c83f153.png)


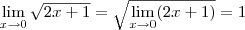


-civil- escreveu:Preciso calcular esse limite pela definição:em p = 1
-civil- escreveu:Percebi que quando escrevi aqui acabei colocando p=1 em vez de p=0.
(...)
Só que o gabarito (7.17 - 1 (b) do Guidorizzi) mostra que a solução é 1.
1. Calcule, pela definição, a derivada da função dada, no ponto dado.
(...)
b)em p = 0.
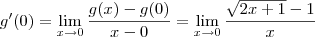 .
. .
.
Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes

 .
.



