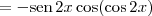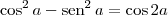por 0 kelvin » Sex Abr 15, 2011 06:50
por 0 kelvin » Sex Abr 15, 2011 06:50
Derivar sen(cos²(x))cos(sen²(x))
Fiz o produto e saiu (sen(cos²(x)))' . cos(sen²(x)) + sen(cos²(x)) . (cos(sen²(x)))'
Daí derivada de sen é cos e cos é -sen.
cos(cos²(x)) . cos(sen²(x)) + sen(cos²(x)) . (-sen(sen²(x)))
Substituindo variável:
cos(x) = u
sen(x) = v
cos(u²) . cos(v²) + sen(u²) . (-sen(v²))
Fiz regra da potência e saiu 2cos(u) . 2cos(v) + 2sen(u) . (-2sen(v))
Mas daí parece que não vai mais pra lugar nenhum.
-
0 kelvin
- Usuário Parceiro

-
- Mensagens: 78
- Registrado em: Dom Out 31, 2010 16:53
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciencias atmosfericas
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Regra da Cadeia] Produto de funções
por Ronaldobb » Sex Out 12, 2012 19:05
- 2 Respostas
- 1350 Exibições
- Última mensagem por DanielFerreira

Sex Out 12, 2012 20:04
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada] regra do produto, da cadeia e trigonometria
por souzalucasr » Sáb Mai 05, 2012 19:33
- 2 Respostas
- 2321 Exibições
- Última mensagem por souzalucasr

Sáb Mai 05, 2012 20:16
Cálculo: Limites, Derivadas e Integrais
-
- Seno e Cosseno de X??
por Leone de Paula » Ter Jul 13, 2010 00:28
- 1 Respostas
- 4659 Exibições
- Última mensagem por Tom

Ter Jul 13, 2010 00:43
Geometria Plana
-
- Lei do seno e cosseno
 por renataf » Sex Dez 03, 2010 11:06
por renataf » Sex Dez 03, 2010 11:06
- 7 Respostas
- 18809 Exibições
- Última mensagem por Lorettto

Sáb Dez 11, 2010 01:17
Trigonometria
-
- Seno e Cosseno
por karen » Qua Mai 16, 2012 22:20
- 1 Respostas
- 3710 Exibições
- Última mensagem por joaofonseca

Qui Mai 17, 2012 08:51
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


![[\textrm{sen}\,(\cos^2 x)\cos (\textrm{sen}^2\,x)]^\prime = [\textrm{sen}\,(\cos^2 x)]^\prime\cos (\textrm{sen}^2\,x) + \textrm{sen}\,(\cos^2 x)[\cos (\textrm{sen}^2\,x)]^\prime [\textrm{sen}\,(\cos^2 x)\cos (\textrm{sen}^2\,x)]^\prime = [\textrm{sen}\,(\cos^2 x)]^\prime\cos (\textrm{sen}^2\,x) + \textrm{sen}\,(\cos^2 x)[\cos (\textrm{sen}^2\,x)]^\prime](/latexrender/pictures/c3cc201534580ec1117bca4d996a898b.png)
![= \cos(\cos^2 x)[\cos^2 x]^\prime\cos (\textrm{sen}^2\,x) - \textrm{sen}\,(\cos^2 x)\textrm{sen}\,(\textrm{sen}^2\,x)[\textrm{sen}^2\,x]^\prime = \cos(\cos^2 x)[\cos^2 x]^\prime\cos (\textrm{sen}^2\,x) - \textrm{sen}\,(\cos^2 x)\textrm{sen}\,(\textrm{sen}^2\,x)[\textrm{sen}^2\,x]^\prime](/latexrender/pictures/6f90183913bfa94ea297392a5083dfdc.png)
![= 2\cos(\cos^2 x)\cos x[\cos x]^\prime\cos (\textrm{sen}^2\,x) - 2\textrm{sen}\,(\cos^2 x)\textrm{sen}\,(\textrm{sen}^2\,x)\textrm{sen}\,x[\textrm{sen}\,x]^\prime = 2\cos(\cos^2 x)\cos x[\cos x]^\prime\cos (\textrm{sen}^2\,x) - 2\textrm{sen}\,(\cos^2 x)\textrm{sen}\,(\textrm{sen}^2\,x)\textrm{sen}\,x[\textrm{sen}\,x]^\prime](/latexrender/pictures/52b989f8a4c13f0ea501274a92926052.png)
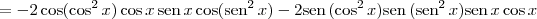
![= -2\textrm{sen}\,x \cos x[\cos(\cos^2 x)\cos (\textrm{sen}^2\,x) + \textrm{sen}\,(\cos^2 x)\textrm{sen}\,(\textrm{sen}^2\,x)] = -2\textrm{sen}\,x \cos x[\cos(\cos^2 x)\cos (\textrm{sen}^2\,x) + \textrm{sen}\,(\cos^2 x)\textrm{sen}\,(\textrm{sen}^2\,x)]](/latexrender/pictures/53ff07c37722f11c6d0bbc7c5d9657b4.png)