 por schmitt » Sáb Abr 09, 2011 15:52
por schmitt » Sáb Abr 09, 2011 15:52
Olá, alguém poderia me ajudar a derivar essa função:
f(x)=xcos(sen(x)) – 1
f'(x)= ?
f''(x)= ?
Obrigado.
Editado pela última vez por
schmitt em Sáb Abr 09, 2011 17:26, em um total de 1 vez.
-
schmitt
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sáb Abr 09, 2011 15:43
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por Molina » Sáb Abr 09, 2011 16:55
por Molina » Sáb Abr 09, 2011 16:55
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por schmitt » Sáb Abr 09, 2011 17:27
por schmitt » Sáb Abr 09, 2011 17:27
Novamente obrigado.
-
schmitt
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sáb Abr 09, 2011 15:43
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Preciso de ajuda com essa questão da Fundação Cesgranrio
por Jesicaa » Qui Mar 12, 2015 11:46
- 2 Respostas
- 3141 Exibições
- Última mensagem por Jesicaa

Dom Mar 15, 2015 00:06
Sistemas de Equações
-
- É preciso saber limite para derivada e integral?
por mineirodointerior » Qui Out 15, 2015 00:34
- 2 Respostas
- 6860 Exibições
- Última mensagem por Cleyson007

Sáb Out 17, 2015 00:04
Cálculo: Limites, Derivadas e Integrais
-
- PRECISO DE AJUDA !
por Layna Cardoso » Ter Mar 16, 2010 20:49
- 1 Respostas
- 2011 Exibições
- Última mensagem por Molina

Ter Mar 16, 2010 21:37
Problemas do Cotidiano
-
- PRECISO DE AJUDA!
por Lurdes » Sex Jul 09, 2010 23:22
- 1 Respostas
- 3418 Exibições
- Última mensagem por Neperiano

Qui Set 29, 2011 16:45
Problemas do Cotidiano
-
- preciso de ajuda...
por apoliveirarj » Qua Jul 21, 2010 12:25
- 5 Respostas
- 4169 Exibições
- Última mensagem por apoliveirarj

Qui Jul 22, 2010 12:52
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



 .
.
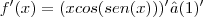
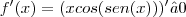




 e posteriormente voltar na função.
e posteriormente voltar na função.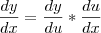
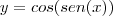 e
e 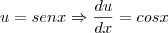 e
e 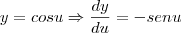







 .
.
 :
: