 por Kelvin Brayan » Qui Mar 10, 2011 12:18
por Kelvin Brayan » Qui Mar 10, 2011 12:18
1.(FUVEST-SP) Dados dois números reais
a e
b que satisfazem as igualdades 1<a<2 e 3<b<5, pode-se afirmar que
A)
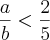
B)
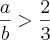
C)
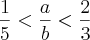
D)
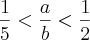
E)
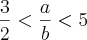
-
Kelvin Brayan
- Colaborador Voluntário

-
- Mensagens: 111
- Registrado em: Dom Fev 20, 2011 16:50
- Localização: Varginha - MG
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Inglês
- Andamento: cursando
 por Elcioschin » Qui Mar 10, 2011 12:23
por Elcioschin » Qui Mar 10, 2011 12:23
a > 1
b > 3
a/b > 1/3
a < 2
b < 5
a/b < 2/5 ----> Alternativa A
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
 por Kelvin Brayan » Qui Mar 10, 2011 15:54
por Kelvin Brayan » Qui Mar 10, 2011 15:54
Valeu !
-
Kelvin Brayan
- Colaborador Voluntário

-
- Mensagens: 111
- Registrado em: Dom Fev 20, 2011 16:50
- Localização: Varginha - MG
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Inglês
- Andamento: cursando
 por LuizAquino » Qui Mar 10, 2011 18:19
por LuizAquino » Qui Mar 10, 2011 18:19
O exercício foi da prova da (FUVEST-1999). O texto original da questão é:
(FUVEST-SP) Dados dois números reais a e b que satisfazem as desigualdades
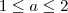
e
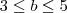
, pode-se afirmar que:
A)
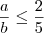
B)
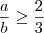
C)
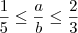
D)
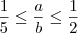
E)
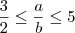
O gabarito oficial é C). Tanto a prova quanto o gabarito estão disponíveis no endereço:
FUVEST Provas 1999http://www.fuvest.br/vest1999/provas/provas.stmAgora, vamos a resolução.
Nós vamos precisar de três propriedades das inequações:
(i) Se
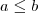
e
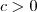
, então
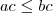
.
(ii) Se
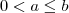
, então
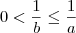
.
(iii) Se

e

, então

.
Multiplicando-se a inequação
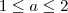
por

(que é um número positivo), obtemos
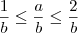
.
Da inequação
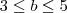
, temos que
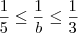
.
Portanto, de
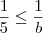
e
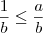
concluímos que
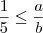
.
Multiplicando-se a inequação
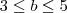
por

(que é um número positivo), obtemos
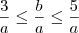
, ou ainda,
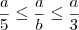
.
Multiplicando-se a inequação
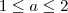
por

, temos que
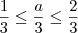
.
Portanto, de
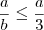
e
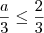
concluímos que
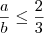
.
Desse modo, temos que
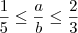
.
Observaçõesa > 1
b > 3
a/b > 1/3
Isso é falso! Note que se a=9/8 e b=9/2 nós temos que 1 < a < 2 e 3 < b < 5, mas a/b < 1/3.
a < 2
b < 5
a/b < 2/5
Isso também é falso! Note que se a=7/4 e b=7/2 nós temos que 1 < a < 2 e 3 < b < 5, mas a/b > 2/5.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Probleminha fuvest
por karen » Ter Nov 27, 2012 15:19
- 3 Respostas
- 1639 Exibições
- Última mensagem por Cleyson007

Ter Nov 27, 2012 15:47
Álgebra Elementar
-
- probleminha
por leandro moraes » Seg Mai 30, 2011 08:06
- 1 Respostas
- 1797 Exibições
- Última mensagem por carlosalesouza

Seg Mai 30, 2011 09:34
Cálculo: Limites, Derivadas e Integrais
-
- probleminha 2
por leandro moraes » Ter Mai 31, 2011 14:41
- 1 Respostas
- 2778 Exibições
- Última mensagem por carlosalesouza

Ter Mai 31, 2011 17:42
Cálculo: Limites, Derivadas e Integrais
-
- Probleminha
por Pjrleal » Qua Mar 14, 2012 10:11
- 1 Respostas
- 2896 Exibições
- Última mensagem por LuizAquino

Qua Mar 14, 2012 15:42
Álgebra Elementar
-
- Probleminha
por karen » Ter Nov 27, 2012 15:55
- 2 Respostas
- 2174 Exibições
- Última mensagem por karen

Ter Nov 27, 2012 16:22
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
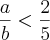
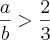
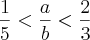
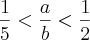
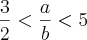

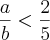
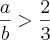
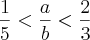
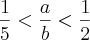
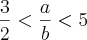



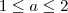 e
e 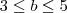 , pode-se afirmar que:
, pode-se afirmar que: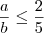
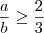
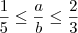
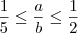
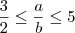
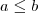 e
e 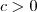 , então
, então 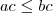 .
.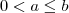 , então
, então 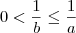 .
. e
e  , então
, então  .
.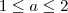 por
por  (que é um número positivo), obtemos
(que é um número positivo), obtemos 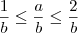 .
.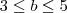 , temos que
, temos que 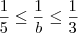 .
.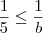 e
e 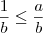 concluímos que
concluímos que 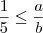 .
.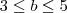 por
por  (que é um número positivo), obtemos
(que é um número positivo), obtemos 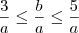 , ou ainda,
, ou ainda, 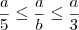 .
.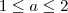 por
por  , temos que
, temos que 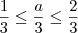 .
.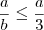 e
e 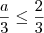 concluímos que
concluímos que 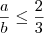 .
.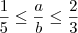 .
.